Rolling of a solid disc on horizontal
Rolling , specifically a pure rolling a classic example of combined translational and rotational motion. While talking the rolling of a solid disc over horizontal ground, actually we discuss a simple case of rolling. Pure rolling refers rolling without slipping. Thus, there is no presence of kinetic friction between point of contact and horizontal surface. Kinetic friction keeps acting until pure rolling is achieved. Static friction may or may not be present in the motion, it depends on on factor whether a force is present throughout the motion or not.
For permanent pure rolling(without slipping), we have conditions i.e. v=\;R\omega and a=\;R\alpha
These are relations between angular speed and linear speed (angular acceleration and tangential acceleration) defines the situation of rolling without slipping.
Rolling of a solid disc on horizontal - A Case of Pure rolling
Here, we are considering an example which incorporates the concept of rolling of a solid disc on horizontal – a case of Pure rolling and its both kinetic energies- translational and rotational. Also, we can use these conditions (of rolling) to relate both kinetics energies of combined translational and rotational motion.
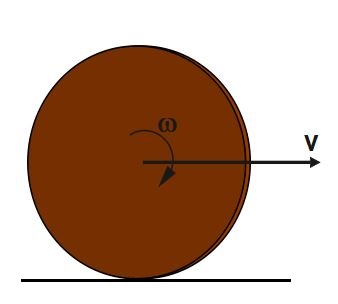
Example - A solid disc is rolling without slipping on a horizontal ground as shown in figure. Its total kinetic energy is 150 J . Its translational and rotational kinetic energies respectively are
(A) 50 J , 100 J
(B)100 J , 50J
(C) 75 J, 75J
(D) 125J , 25J
Solution
As we know that, for pure rolling(without slipping) v=\;R\omega

\frac{K.E._R}{K.E_T}=\frac{{\displaystyle\frac12}I\;\omega^2}{{\displaystyle\frac12}m\;v^2}
\frac{K.E._R}{K.E_T}=\;\frac{\displaystyle\frac12\left(mK^2\right)\;\omega^2}{\displaystyle\frac12m\;v^2}
\frac{K.E._R}{K.E_T} =\frac{\displaystyle K^2\;\omega^2}{\displaystyle v^2}
\frac{K.E._R}{K.E_T}=\frac{\displaystyle K^2\;\omega^2}{\displaystyle{(R\omega)}^2}=\frac{\displaystyle K^2\;\omega^2}{\displaystyle R^2\;\omega^2}
\frac{K.E._R}{K.E_T}=\frac{\displaystyle K^2\;}{\displaystyle R^2\;}.......(1)
Now, I=\;\frac12m\;R^2=m\;K^2\; where\; K \;is \;radius\; of\; Gyration
\Rightarrow\frac{K^2}{R^2}=\frac12.......(2)
\Rightarrow\;\frac{K.E._R}{K.E_T}=\frac{K^2}{R^2}=\frac12 [from (1) and (2)]
\Rightarrow\;\frac{K.E._R}{K.E_T}=\frac12
\Rightarrow\ K.E_T=\;\left(\frac2{1+2}\right)\;K.E._{total}
\Rightarrow\ K.E_T=\;\left(\frac2{3}\right)\;*150
\Rightarrow\ K.E_T= 2* 50 = 100J
Similarly, K.E_R=\;\left(\frac1{1+2}\right)\;K.E._{total}
\Rightarrow K.E_R=\;\left(\frac1{1+2}\right)\;*150
\Rightarrow K.E_R=\;\left(\frac1{3}\right)\;*150
\Rightarrow K.E_R=1*50=50J
(B) is correct option
Conclusion: -
From above discussion , we can easily understand that the basic knowledge of moment of inertia, kinetic energies and condition of rolling (without slipping) helps us to solve problems based on such concepts. For more question visit the page Physics-XI Mechanics
