Count of Beats : How to determine the frequency of Unknown Tuning Fork

Beats is a popular word among musician. Using beats formation concept, they tune their instruments while playing them against some standard frequency. All instruments come into tune when beats disappear. Now the instruments sound with same standard frequency which implies that there has been a change or improvement in the way all the instruments are synchronized to achieve a uniform frequency.
Beat frequency can be simply termed as number of beats produced per second. Beat frequency can be easily calculated by formula :
f_{beat}=\;\left|f_1-f_2\right|
Here, f_{beat} is beat frequency (number of beats produced per second) and f_1 and f_2 are frequency of two different sounds/tuning forks.
For example, if two tuning forks have frequencies of 440 Hz and 442 Hz, the beat frequency would be \left|\;440-442\;\right|=2 beats per second. The human ear should be able to detect and perceive these two beats.
When the difference in frequencies between two sound sources is large, the resulting beats become less perceptible to the human ear. Beats are more pronounced and easily perceived when the frequency difference is smaller. As the frequency difference increases, the rate of beats also increases, but the individual beats become less distinguishable and may merge into a continuous, rapidly fluctuating sound.
The ability to perceive beats is not solely dependent on the numerical difference in frequencies but also on the overall frequency range and sensitivity of an individual’s hearing. In many cases, people can perceive beats with differences well below 10 Hz.
Determination of Unknown Frequency by using concept of Beats
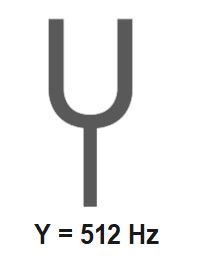

Lets us assume that we have two tuning forks Y and X . The frequency of Y is known to be 512Hz whereas the frequency of X is unknown. When Y is sounded with X it produces 4 beats per second.
f_{beat}=\;\left|f_1-f_2\right| =4
Using above formula and putting f_{1}= 512Hz , we can say that the possible values of frequencies of unknown tuning fork are 512-4\;=\;508\;Hz\;and\;512+4\;=516Hz
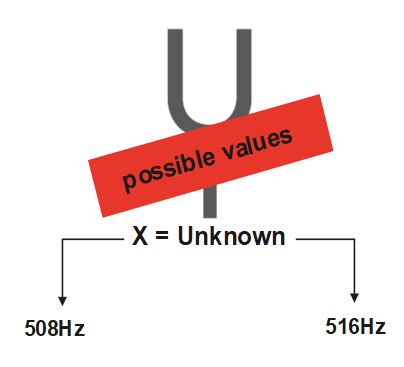
Now, it is to decide that which values is actual value of frequncy of unknown tuning fork X among 508Hz and 516Hz.
We have two method to assign correct value to unknown frequency X.
1.By Loading Unknown Tuning Fork (X) with wax
Loading of wax makes tuning heavier which leads to decrease in frequency. Thus, the frequency of unknown tuning fork X after loading wax, decreases. Let us say these decreased values are 507 Hz (for 508 Hz) and 515Hz ( for 516Hz).
Therefore, new possible beats when X (on loading) with decreased frequencies is sounded with Y are:
Case-1:- \left|512-\;507\right|=\;5\; beats per second (note that beats increases in this case )
Case-2:- \left|512-\;515\right|=\;3\; beats per second (note that beats decreases in this case )
(a).On loading wax, again sound the unknown tuning fork X with Y, if beats increases as in case (1), then 508Hz is actual value of unknown frequency, X=508Hz
(b). On loading wax, again sound the unknown tuning fork X with Y, if beats decrease as in case (2), then 516 Hz is actual value of unknown frequency, X=516 Hz
Sample Question– Tuning fork A when sounded with a tuning fork B of frequency 480 Hz gives 5 beats per second. When the prongs of A are loaded with wax, it gives 3 beats per second. Find the original frequency of A.
Solution:-
Given that , known frequency (of fork B) = 480 Hz
Let Unknown frequency of fork A = x
They produce beat when sounded together = 5
Therefore, possible values of x are 480- 5 = 475 Hz and 480+5 = 485 Hz
Now, we have to check which value among 475Hz and 485Hz is correct?
As, this is a case of loading wax , therefore, frequency of A (on loading wax) decreases. Hence, two possible values are 474 (say) and 484(say) respectively.
Therefore, new possible beats when A (on loading) with decreased frequencies is sounded with B(480Hz) are:
Case-1:- \left|480-\;474\right|=\;6\; beats per second (note that beats increase in this case )
Case-2:- \left|480-\;484\right|=\;4\; beats per second (note that beats decrease in this case )
It is already given that on loading fork B produces 3 beats per second with fork A which means beats per second are decreasing.
That is why we will chose the second case which shows decrease in beats per second. Finally, we assign 485 Hz as actual value of unknown fork A.
Answer of this question is f_{A}= 485Hz
Questions for practice
Question 1 – A tuning fork of known frequency 440 Hz is sounded simultaneously with another tuning fork. The beat frequency observed is 4 Hz. When a small piece of wax is loaded onto the second tuning fork, the beat frequency becomes 2 Hz. Determine the frequency of the second tuning fork.
Question-2 A tuning fork of unknown frequency is sounded simultaneously with another tuning fork of known frequency 450 Hz. The beat frequency observed is 5 Hz. To make the beats disappear, a small piece is filed from the prongs of the unknown tuning fork. After filing, the beat frequency reduces to 1 Hz. Determine the frequency of the unknown tuning fork before and after filing.
Now, you can try the above questions by yourself and send us the your answers. We would respond to answers in comment section.
2.By Filing Unknown Tuning Fork (X)
If the prong of fork is filed a little, its mass gets reduced and its frequency increases. Therefore, frequency of filed unknown tuning fork X decreases. Suppose that increased values are 510Hz Hz (for 508 Hz) and 518Hz ( for 516Hz).
Therefore, new possible beats when X (filed) with increased frequencies is sounded with Y are:
Case-1:- \left|512-\;510\right|=\;2\; beats per second (note that beats decreases in this case )
Case-2:- \left|512-\;518\right|=\;6\; beats per second (note that beats increases in this case )
(a).After filing, again sound the unknown tuning fork X with Y, if beats increases as in case (2), then 516Hz is actual value of unknown frequency, X=516Hz
(b). After filing, again sound the unknown tuning fork X with Y, if beats decrease as in case (1), then 508 Hz is actual value of unknown frequency, X=508 Hz
Sample Question– A tuning fork P produces 8 beats per second with another tuning fork Q of frequency 342Hz. When the prongs of the tuning fork P are filed a little, the number of beats produced per second decreases to 4. Find the frequency of the tuning fork P before filing its prongs.
Solution:-
Given that , known frequency (of fork Q) = 342 Hz
Let Unknown frequency of fork P = x
They produce beat when sounded together before filing = 8
Therefore, possible values of x are 342- 8 = 334 Hz and 342+8 = 350 Hz
Now, we have to check which value among 334Hz and 350Hz is actual frequency of P before filing?
As, this is a case of filing, therefore, frequency of P (on filing) increases. Hence, two possible values are 337 (say) and 353(say) respectively.
Therefore, new possible beats when P (after filing) with increased frequencies is sounded with Q(342 Hz) are:
Case-1:- \left|342-\;337\right|=\;5\; beats per second (note that beats decrease in this case )
Case-2:- \left|342-\;353\right|=\;9\; beats per second (note that beats increase in this case )
It is already given that on loading fork B produces 4 beats per second with fork A which means beats per second are decrease.
That is why we will chose the first case which shows decrease in beats per second. Finally, we assign 334 Hz as actual value of unknown fork P.
Answer of this question is f_{P}= 334Hz

Quite an elaborate and well explained topic. Really showcases the author’s magnificent ability in making tricky subject like this (beats) easier to understand. One of the best explanations on the internet for sure.
odit id et ratione libero voluptatem omnis nihil dolorum corporis quos et quisquam optio eligendi odio molestias. sit sapiente voluptate iure qui explicabo et maxime fugiat.
“Plenum est doloris et cruciatus, ubi nullus valor corporis et animae est. Homines semper dolores elegerunt et eos tolerare discere debent. Sapientem esse significat felicitatem augere et omnem vitae momentam plene vivere intellegere.”
velit asperiores impedit asperiores rerum possimus eum voluptates excepturi accusamus. in autem quia ipsum odio ut laborum voluptatibus temporibus hic veniam recusandae. beatae sit eaque fugit eius re
“Inter certamina et provocationes quas vita nobis obicit, conatur pervadere sine accusationibus negativis succumbens. Tamen, contemptus eius adversus difficultates facit ut momenta felicitatis et occasionem necessarias reconciliandi amittat. Vere beati sunt qui super destinatas molestias se erigere quaerunt.”
autem sapiente exercitationem tenetur nihil nihil sint dolores facilis eaque distinctio blanditiis quod saepe voluptatem ut minima. ipsa nesciunt sit nam placeat quo sit sequi rerum quis aut neque. qu
voluptatum non vel temporibus repellendus sit et. tempora id et tempore delectus ut aut est. laboriosam minima blanditiis id voluptas recusandae quibusdam impedit eligendi quia explicabo eos est quia
odit ipsa rerum necessitatibus sit voluptatem eius sunt illum molestias. reiciendis rerum provident vel et perspiciatis. aut maxime est natus ex quod inventore laudantium officiis officiis voluptatem