Top 5 Fluid Mechanics problems for IIT-JEE NEET
Q1. from "Top 5 Fluid Mechanics problems for IIT-JEE NEET"
Q1.The tension in a string holding a solid block below the surface of a liquid (of density greater than that of solid) as shown in the figure is T_o when the system is at rest. What will be the tension in the string if the system has upward acceleration a.
T_o\frac ag
T_o\left(1-\frac ag\right)
T_o\left(1+\frac ag\right)
T_o\left(\frac ag-1\right)
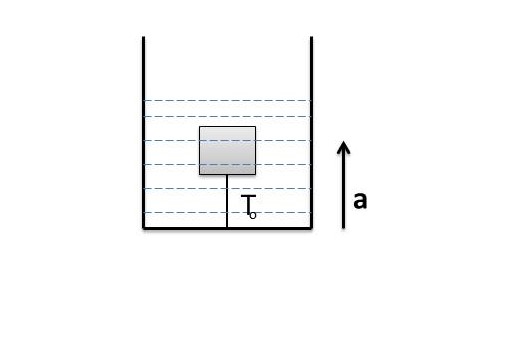
Q1.The tension in a string holding a solid block below the surface of a liquid (of density greater than that of solid) as shown in the figure is T_o (To) when the system is at rest. What will be the tension in the string if the system has upward acceleration a.
(A) T_o\frac ag
(B) T_o\left(1-\frac ag\right)
(C) T_o\left(1+\frac ag\right)
(D) T_o\left(\frac ag-1\right)

Solution
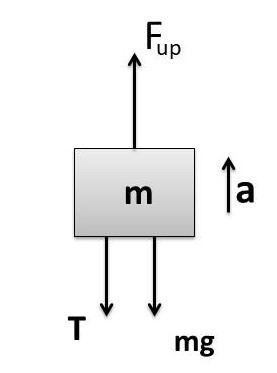
At Equilibrium (Rest), Free body diagram of block
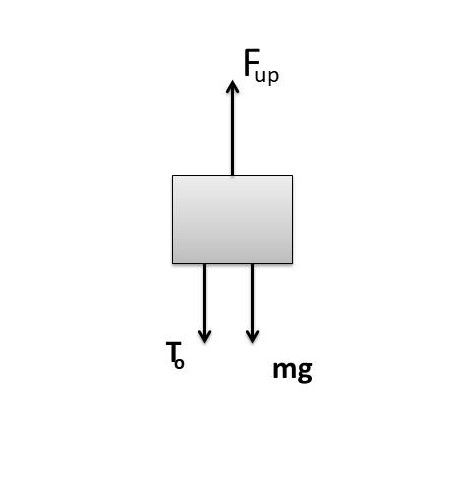
T_0+mg=F_{up}
T_o+V\rho_Sg=\;\;V\rho_Lg\\
Vg(\;\rho_L-\;\rho_S)\;=T_o
\rho_L-\;\rho_S=\frac{T_o}{Vg}\;-----(1)
Free body diagram of block when it moves upwards.
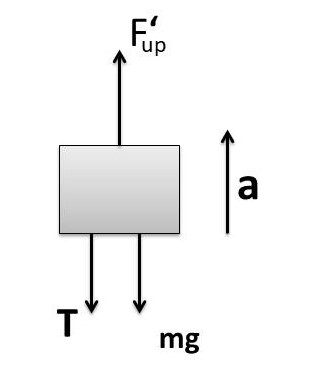
When system moves up with acceleration 'a' then effective weight of fluid displaced also changes which is called apparent weight (of fluid displaced).
F_{up}^I=V\;\rho_L\;g_{eff}
Since, the system is moving up with acceleration 'a' .Thus, \\g_{eff}=\;g+a-----(2)
As 'a' be the acceleration of system , Use Free body diagram of the moving block
F_{net}=F_{up}^I-mg-T
Therefore, ma=V\;\rho_L\;g_{eff}-mg-T
m(\;a\;+g)=V\;\rho_L\;g_{eff}\;-T
V\;\rho_S\;(\;a\;+g)=V\;\rho_L\;g_{eff}\;-T
Now use (2), V\;\rho_S\;(\;g+a)=V\;\rho_L\;(g+a)\;-T
V\;\rho_S\;(\;g+a)=V\;\rho_L\;(g+a)\;-T
T=\;V(g+a)\;(\;\rho_L-\;\rho_S)
Using (1), T=\;V(g+a)\;({\textstyle\frac{T_o}{V\;g}})\;
T=\;\;T_o\left(1+\frac ag\right)\\
Ans. (C) is correct option
Q2. from "Top 5 Fluid Mechanics problems for IIT-JEE NEET"
Q2. A small body of density ρ is dropped from rest at a height h into a lake of density σ , where σ > ρ . What would be of the acceleration of body till it moves inside the lake? (Neglect all dissipative effects)
g\left(\frac\sigma\rho-1\right)\;downwards
g\left(\frac\sigma\rho-1\right)\;upwards
g\left(\frac\sigma\rho\right)\;downwards
g\left(\frac\sigma\rho\right)\;upwards
Q2.A small body of density ρ is dropped from rest at a height h into a lake of density σ , where σ > ρ . What would be of the acceleration of body till it moves inside the lake? (Neglect all dissipative effects)
(A) g\left(\frac\sigma\rho-1\right)\;downwards
(B) g\left(\frac\sigma\rho-1\right)\;upwards
(C) g\left(\frac\sigma\rho\right)\;downwards
(D) g\left(\frac\sigma\rho\right)\;upwards
Solution
Let V = Volume of body
\rho = density of body
\sigma = density of lake water
Thus, m=\;\rho\;V
As the density of liquid is more than that of body( σ > ρ), Therefore the body has tendency to float on the liquid because of larger upwards force in comparison to that of weight of body. Hence, net force will be upwards.
W know that F_{up}=V\;\sigma g\;
According to Newton's 2nd law of motion, we can write
F_{net}= F_{up}-mg (upwards)
F_{net}= V\sigma g -V \rho g
ma = V\sigma g -V \rho g
V\rho a = V\sigma g -V \rho g
a=\frac{V(\sigma-\rho)g}{V\rho}
a=\frac{(\sigma-\rho)g}{\rho}
a=g\left(\frac\sigma\rho-1\right)\;upwards
(B) is correct option

Q3. from "Top 5 Fluid Mechanics problems for IIT-JEE NEET"
Q3.A partially immersed solid block of \rho_s is floating in a liquid of density \rho_L as shown in figure. If beaker container moves up with positive acceleration 'a' , what is correct statement about the block?
It sinks more inside the liquid
It sinks lesser inside the liquid
It neither sinks more nor lesser inside the liquid
Can not be predicted as data is insufficient
Q3.A partially immersed solid block of \rho_s is floating in a liquid of density \rho_L as shown in figure. If beaker container moves up with positive acceleration 'a' , what is correct statement about the block ?

Solution
Let V_{in} = Volume of block immersed in the liquid
For Equilibrium of rest, see FBD as shown aside
F_{up}=V_{in}\;\rho_Lg\;=\;mg
V_{in}\;\rho_Lg\;=\;V\;\rho_S\;g\;
\;\frac{V_{in}}V\;=\frac{\rho_S}{\rho_L}
Therefore, fraction of volume inside the liquid is-
\;\frac{V_{in}}V\;=\frac{\rho_S}{\rho_L}.....(1)
When block is moving up , the FBD is shown in figure
\;\\F_{up}^I=V_{in}^I\;\rho_L\;g_{eff}\\
F_{up}^I=V_{in}^I\;\rho_L\;(g+a).....(2)
F_{net}=F_{up}^I-mg
ma =F_{up}^I-mg
F_{up}^I=m(g+a)
F_{up}^I=V\;\rho_S\;(g+a)\\....(3)
From (2) and (3), V_{in}^I\;\rho_L\;(g+a)=V\;\rho_S\;(g+a)
\;\frac{V_{in}^I}V\;=\frac{\rho_S}{\rho_L}
\;\frac{V_{in}}V\;=\frac{\rho_S}{\rho_L}=\;\frac{V_{in}^I}V\;
Hence, fraction of volume immersed is again equal to \frac{\rho_S}{\rho_L}. It means immersed volume remains same .
Ans. (C) is correct option
Q4. from "Top 5 Fluid Mechanics problems for IIT-JEE NEET"
Q4.A block of mass 1 kg and density 0.8 g/cm^3 is held stationary with the help of a string as shown in figure. The block is completely immersed into the water filled in tank.If the tank is accelerating vertically upwards with an acceleration a = 2m/s^2. Find the tension in the string.
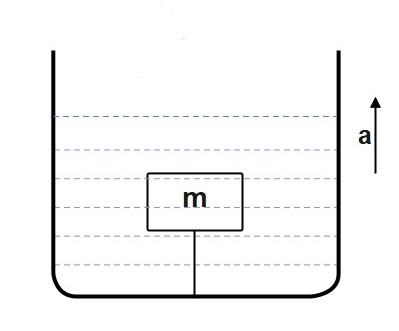
A block of mass 1 kg and density 0.8 g/cm^3 is held stationary with the help of a string as shown in figure. The block is completely immersed into the water filled in tank.If the tank is accelerating vertically upwards with an acceleration a = 2 m/s^2.
(i) Find the tension in the string.

(A) 3 N
(B) 2 N
(C) 3.5 N
(D) 5.5 N
Solution
Let V = Volume of body
\rho = density of block = 0.8 \frac{g}{cm^3}=800\frac{kg}{m^3}
\sigma = density of water =1000\frac{kg}{m^3}
We know that, the mass of block= m=\;\rho\;V
\rho=\frac mV
V=\frac m\rho
We know that F_{up}=V\sigma(g+a)\;
\Rightarrow F_{up}=\frac m\rho\sigma(g+a)\;
\Rightarrow F_{up}=\frac1{800}\ast1000\ast(10+2)=15N
According to Newton's 2nd law of motion, we can write
F_{net}= F_{up}-T- mg
ma= F_{up} -T- mg
1*2= 15-T-1*10
2= 15 - T- 10
T= 15 - 10-2=3N
(A) is correct option
Q5. from "Top 5 Fluid Mechanics problems for IIT-JEE NEET"
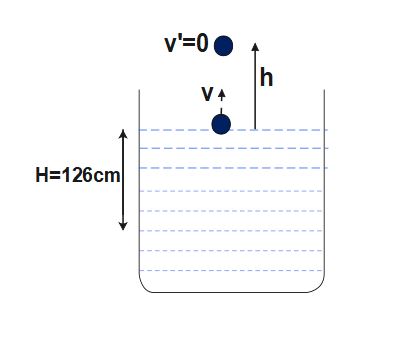
Q5.A wooden ball of density 900 kg / m^{3} is immersed in a liquid of density 1200 kg / m^{3} to a depth of 126 cm and the released. The height h above the surface of which the ball rises will be

A wooden ball of density 900 kg / m^{3} is immersed in a liquid of density 1200 kg / m^{3} to a depth of 126 cm and the released. The height h above the surface of which the ball rises will be
(A) 40 cm
(B) 42 cm
(C) 45 cm
(D) 50 cm
Solution
Let V = Volume of ball
Given that, \rho = density of ball= 900\frac{kg}{m^3}
\sigma = density of liquid =1200\frac{kg}{m^3}
As, the density of ball = \rho=\frac mV
m=V\rho
We know that F_{up}=V\sigma g\;
According to Newton's 2nd law of motion, we can write
F_{net}= F_{up}-mg
ma= V\sigma g - V\rho g
V\rho a= V\sigma g - V\rho g
a=\;\frac{V\sigma g-V\rho g}{V\rho}
a=\;\frac{(\sigma-\rho)g}\rho
a=\;\frac{(1200-900)g}{900}
a=\;\frac{(300)g}{900}
a=\;\frac{g}{3}
Now, u=0 (because the ball is released from rest)
When ball reaches to surface, S= 126 cm = 1.26 m. Also, let us assume that it attains velocity v at top surface.
According to Kinematics Equation of U.A.M., v^2-u^2=2aS
\Rightarrow v^2-0^2=2\left(\frac g3\right)\;\left(1.26\right)
\Rightarrow v^2=0.84 g .....(1)
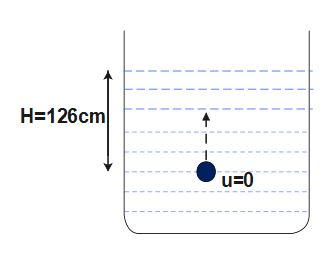
h= height the ball attains when it rises up with velocity v from top surafce
Since , the ball rises up vertically under the effect of gravity, so it would come to rest momentarily when it attains height 'h'
v^{'}=0
A =-g
(-ve sign appears as the diraction of acceleration is against motion)
Again,apply V^2-U^2=2AS
\Rightarrow\;v'^2-v^2=2(-g) h
\Rightarrow\;0^2-v^2=2(-g) h
\Rightarrow\ v^2=2gh ....(2)
From (1) and (2), we get,
0.84g = 2gh
h=\frac{0.84g}{2g}
h=0.42m=42cm
(B) is correct option