Maximum compression in the spring

Q.What is the maximum compression in the spring, if the lower block is shifted to rightward with acceleration a. (Given that all surfaces are smooth as shown).

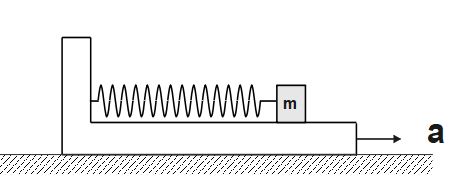
(A) $\frac{ma}k$

(B) $\frac{2ma}k$

(D) $\frac{ma}{2k}$

Solution

Let us assume that the upper block of mass 'm' displaces by distance 'x' towards leftward with velocity 'v' (w.r.t to lower block) when lower block is shifted towards rightward with acceleration a.

We can solve this problem by two methods (1) Force Method (2) Energy Method from non-inertial frame of reference (Lower plank/block) .

Force Method

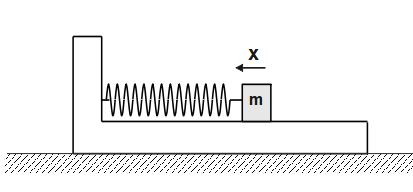
Acc. to Newton's 2nd law of motion,

$F_{net}=F_{pseu}-F_{spring}$

$F_{net}=ma- kx$

$m a_1 =ma- kx$

$m \frac{\operatorname dv}{\operatorname dt}=ma\;-\;kx$

$mv\frac{\operatorname dv}{\operatorname dx}=ma\;-\;kx$

$mv\;dv=\left(ma\;-\;kx\right)\;dx$

Integrating both sides

$m \int_{v_i}^{v_f}\;vdv=\int_{x_i}^{x_f}\left(ma\;-\;kx\right)\;dx$

$m\int_{0}^{0}\;vdv=\int_{0}^{x_o}\left(ma\;-\;kx\right)\;dx$

$m\left[\frac{v^2}2\right]_0^0=\;ma\;\left[x\right]_0^{x_0}-k\left[\frac{x^2}2\right]_0^{x_o}$

$m(0-0)=\;ma\;\left(x_o-0\right)-\;\frac12k\;\left(x_o^2-0\right)$

$0=\;ma x_o - \;\frac12k\ x_o^2$

$ma x_o = \frac12k\ x_o^2$

$2ma= k x_{o}$

$x_o=\frac{2ma}k$

(B) is correct option

let $a_1$ be the acceleration of upper block w.r.t the lower block

FBD of upper block from lower block reference frame

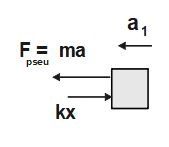
Boundary conditions for integration:

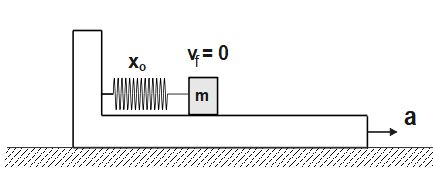
Initially, the upper block is at rest when x=0, therefore $v_{i}=0$

When the spring has maximum compression $x_{o}$ , again the block becomes stationary w.r.t. lower block.

So, $v_{f}=0$ , $when x=x_{o}$

Alternate Method

We can also solve this problem by Energy Method from non-inertial frame of reference (Lower plank/block) . We will apply Work-Energy theorem from lower block frame of reference.

Energy Method

We can apply Work-Energy theorem for initial and final positions of upper block w.r.t. lower block

Since, at initial position the upper block is at rest, therefore $v_{i}=0$

When the spring has maximum compression $x_{o}$ , again the block becomes stationary w.r.t. lower block. So, also $v_{f}=0$

Acc. to Work-Energy Theorem,

$W.D_{net \;by\;all\;forces}\;=\triangle K.E.\;$

$W.D._{pseudo}\;\;+\;W.D._{spring}\;=\;\frac12m\;v_f^2-\frac12m\;v_i^2$

$W.D._{pseudo}\;\;+\;W.D._{spring}\;=\;\frac12m\;0^2-\frac12m\;0^2$

$\Rightarrow\;ma\;x_o-\;\frac12k\;x_o^2=0$

$\Rightarrow\;ma\;x_o=\;\frac12k\;x_o^2$

$\Rightarrow\;ma\;=\;\frac12k\;x_o$

$\Rightarrow\;x_o=\frac{2ma}k$

(B) is correct option

For more mechanics problems visit our question bank page

We must know that the work done by conservative forces is

$\;W.D._{cons}\;=-\triangle U$

$\;\Rightarrow\;W.D._{spring}\;=-\triangle U$

$\;\Rightarrow W.D._{spring}\;=-\;\frac12k\;x_{o}^2$

And, $W.D._{pseu}={\overrightarrow{F\;}}_{pseu}.\overrightarrow{x_o}$

$\Rightarrow W.D._{pseu}=F_{pseu}\;x_{o\;}\cos0^o$

$\Rightarrow W.D._{pseu}=ma\;x_{o\;}$

Key concept to solve above problem

Frame of reference
Pseudo force
Work-Energy Theorem
Condition for Maximum compression in the spring

Frame of reference

In mechanics , the frame of reference is directly tied to the perspective of an observer. A frame of reference is essentially a set of coordinate axes and a set of observational rules that allow an observer to quantify and describe the motion of objects. The observer’s point of view or choice of reference frame influences how the physical phenomena are described and analyzed. All of us know that the motion is a relative concept. So, frame of reference which observer chooses directly affect the observation.

For example, if you are driving to towards Taj Mahal and after some time a fellow passenger ask when will Taj Mahal come whereas he knows you are moving towards destination!
It does indeed reflect a perspective from the car’s frame of reference. The passenger is implicitly treating the car as the stationary reference point, making it appear as though the Taj Mahal is approaching them. From the frame of reference inside the car, the surroundings outside might seem to be moving, creating the perception that the destination (Taj Mahal) is approaching. Meanwhile, from an external frame of reference, such as someone on the ground, it would be clear that the car is moving towards the stationary Taj Mahal.

Let’s consider the other (following) example which helps you to grasp the concept.

If you are inside a car moving at a constant speed and you throw a ball straight up, from your perspective inside the car, the ball will appear to go straight up and down. However, an observer outside the car, seeing the entire motion, would notice that the ball follows a parabolic trajectory due to the combined motion of the car and the ball. There are mainly two type of frame of references

(1) Inertial Frame of Reference:

An inertial frame of reference is often preferred when studying the laws of mechanics. In an inertial frame, an object either remains at rest or moves with a constant velocity unless acted upon by an external force.
Newton’s laws of motion are formulated with respect to inertial frames.

(2) Non-Inertial Frames:

In non-inertial frames (accelerating or rotating frames), additional forces called fictitious forces may appear. These forces are not “real” forces but are necessary for describing motion accurately from the perspective of an observer in a non-inertial frame.
Common example include centrifugal

Pseudo force

A pseudo force is an apparent or fictitious force introduced in non-inertial reference frames to account for observed accelerations, allowing the application of Newton’s laws of motion as if the frame were inertial.

Work Energy Theorem

The work-energy theorem states that the work done on an object by all forces (conservative, non conservative, pseudo force etc. ) is equal to the change in its kinetic energy. In equation form, it can be expressed as:

$W = Δ K E$

Condition for maximum compression in the spring

When a block is attached to a spring and compressed to its maximum, the block will momentarily come to rest with respect to the reference frame to which the spring is attached., assuming no external forces act on the block after it reaches its maximum compression.

When the spring is compressed to its maximum, the potential energy stored in the spring is at its maximum, and this energy is then converted into kinetic energy as the block is released. At the point of maximum compression, the block’s velocity becomes zero before it starts moving in the opposite direction due to the restoring force of the spring. The momentary pause at maximum compression in the spring, is indeed a point where the block stops with respect to the frame to which the spring is attached.

blogmedia

3 August 2024 at 12:01 AM

I was recommended this website by my cousin I am not sure whether this post is written by him as nobody else know such detailed about my difficulty You are wonderful Thanks

temp mail education

4 August 2024 at 2:48 PM

Temp mail Pretty! This has been a really wonderful post. Many thanks for providing these details.

Baccarat

6 August 2024 at 6:30 PM

My brother suggested I might like this blog He was totally right This post actually made my day You can not imagine simply how much time I had spent for this info Thanks

Your Coaching Institute

Maximum compression in the spring

Q.What is the maximum compression in the spring, if the lower block is shifted to rightward with acceleration a. (Given that all surfaces are smooth as shown).

Table of Contents

Solution

Let us assume that the upper block of mass 'm' displaces by distance 'x' towards leftward with velocity 'v' (w.r.t to lower block) when lower block is shifted towards rightward with acceleration a.

We can solve this problem by two methods (1) Force Method (2) Energy Method from non-inertial frame of reference (Lower plank/block) .

Force Method

Acc. to Newton's 2nd law of motion,

F_{net}=F_{pseu}-F_{spring}

F_{net}=ma- kx

m a_1 =ma- kx

m \frac{\operatorname dv}{\operatorname dt}=ma\;-\;kx

mv\frac{\operatorname dv}{\operatorname dx}=ma\;-\;kx

mv\;dv=\left(ma\;-\;kx\right)\;dx

Integrating both sides

m \int_{v_i}^{v_f}\;vdv=\int_{x_i}^{x_f}\left(ma\;-\;kx\right)\;dx

m\int_{0}^{0}\;vdv=\int_{0}^{x_o}\left(ma\;-\;kx\right)\;dx

m\left[\frac{v^2}2\right]_0^0=\;ma\;\left[x\right]_0^{x_0}-k\left[\frac{x^2}2\right]_0^{x_o}

m(0-0)=\;ma\;\left(x_o-0\right)-\;\frac12k\;\left(x_o^2-0\right)

0=\;ma x_o - \;\frac12k\ x_o^2

ma x_o = \frac12k\ x_o^2

2ma= k x_{o}

x_o=\frac{2ma}k

(B) is correct option

let a_1 be the acceleration of upper block w.r.t the lower block

FBD of upper block from lower block reference frame

Boundary conditions for integration:

Initially, the upper block is at rest when x=0, therefore v_{i}=0

When the spring has maximum compression x_{o}, again the block becomes stationary w.r.t. lower block.

So, v_{f}=0 , when x=x_{o}

Alternate Method

We can also solve this problem by Energy Method from non-inertial frame of reference (Lower plank/block) . We will apply Work-Energy theorem from lower block frame of reference.

Energy Method

We can apply Work-Energy theorem for initial and final positions of upper block w.r.t. lower block

Since, at initial position the upper block is at rest, therefore v_{i}=0

When the spring has maximum compression x_{o}, again the block becomes stationary w.r.t. lower block. So, also v_{f}=0

Acc. to Work-Energy Theorem,

W.D_{net \;by\;all\;forces}\;=\triangle K.E.\;

W.D._{pseudo}\;\;+\;W.D._{spring}\;=\;\frac12m\;v_f^2-\frac12m\;v_i^2

W.D._{pseudo}\;\;+\;W.D._{spring}\;=\;\frac12m\;v_f^2-\frac12m\;v_i^2

W.D._{pseudo}\;\;+\;W.D._{spring}\;=\;\frac12m\;*0^2-\frac12m\;*0^2

\Rightarrow\;ma\;x_o-\;\frac12k\;x_o^2=0

\Rightarrow\;ma\;x_o=\;\frac12k\;x_o^2

\Rightarrow\;ma\;=\;\frac12k\;x_o

\Rightarrow\;x_o=\frac{2ma}k

(B) is correct option

For more mechanics problems visit our question bank page

We must know that the work done by conservative forces is

\;W.D._{cons}\;=-\triangle U

\;\Rightarrow\;W.D._{spring}\;=-\triangle U

\;\Rightarrow W.D._{spring}\;=-\;\frac12k\;x_{o}^2

And, W.D._{pseu}={\overrightarrow{F\;}}_{pseu}.\overrightarrow{x_o}

\Rightarrow W.D._{pseu}=F_{pseu}\;x_{o\;}\cos0^o

\Rightarrow W.D._{pseu}=ma\;x_{o\;}

Key concept to solve above problem

Frame of reference

Pseudo force

Work Energy Theorem

Condition for maximum compression in the spring

3 thoughts on “What is the maximum compression in the spring, if the lower block is shifted to rightward with acceleration a. (Given that all surfaces are smooth as shown).”

Leave a Comment Cancel Reply

Contact Us

Follow Us

Why Us

Services

website policy

Disclaimer

Hyperlinking policy

Feedback

Phase - 6 , Sector- 56 ,

Mohali (Punjab)/ Chandigarh-160055

India

Copyright © 2024, PCM TUTORIALS, All Rights are Reserved

$F_{net}=F_{pseu}-F_{spring}$

$F_{net}=ma- kx$

$m a_1 =ma- kx$

$m \frac{\operatorname dv}{\operatorname dt}=ma\;-\;kx$

$mv\frac{\operatorname dv}{\operatorname dx}=ma\;-\;kx$

$mv\;dv=\left(ma\;-\;kx\right)\;dx$

$m \int_{v_i}^{v_f}\;vdv=\int_{x_i}^{x_f}\left(ma\;-\;kx\right)\;dx$

$m\int_{0}^{0}\;vdv=\int_{0}^{x_o}\left(ma\;-\;kx\right)\;dx$

$m\left[\frac{v^2}2\right]_0^0=\;ma\;\left[x\right]_0^{x_0}-k\left[\frac{x^2}2\right]_0^{x_o}$

$m(0-0)=\;ma\;\left(x_o-0\right)-\;\frac12k\;\left(x_o^2-0\right)$

$0=\;ma x_o - \;\frac12k\ x_o^2$

$ma x_o = \frac12k\ x_o^2$

$2ma= k x_{o}$

$x_o=\frac{2ma}k$

let $a_1$ be the acceleration of upper block w.r.t the lower block

Initially, the upper block is at rest when x=0, therefore $v_{i}=0$

When the spring has maximum compression $x_{o}$ , again the block becomes stationary w.r.t. lower block.

So, $v_{f}=0$ , $when x=x_{o}$

Since, at initial position the upper block is at rest, therefore $v_{i}=0$

When the spring has maximum compression $x_{o}$ , again the block becomes stationary w.r.t. lower block. So, also $v_{f}=0$

$W.D_{net \;by\;all\;forces}\;=\triangle K.E.\;$

$W.D._{pseudo}\;\;+\;W.D._{spring}\;=\;\frac12m\;v_f^2-\frac12m\;v_i^2$

$W.D._{pseudo}\;\;+\;W.D._{spring}\;=\;\frac12m\;v_f^2-\frac12m\;v_i^2$

$W.D._{pseudo}\;\;+\;W.D._{spring}\;=\;\frac12m\;0^2-\frac12m\;0^2$

$\Rightarrow\;ma\;x_o-\;\frac12k\;x_o^2=0$

$\Rightarrow\;ma\;x_o=\;\frac12k\;x_o^2$

$\Rightarrow\;ma\;=\;\frac12k\;x_o$

$\Rightarrow\;x_o=\frac{2ma}k$

$\;W.D._{cons}\;=-\triangle U$

$\;\Rightarrow\;W.D._{spring}\;=-\triangle U$

$\;\Rightarrow W.D._{spring}\;=-\;\frac12k\;x_{o}^2$

And, $W.D._{pseu}={\overrightarrow{F\;}}_{pseu}.\overrightarrow{x_o}$

$\Rightarrow W.D._{pseu}=F_{pseu}\;x_{o\;}\cos0^o$

$\Rightarrow W.D._{pseu}=ma\;x_{o\;}$