Kinematics: Understanding Uniform Motion
What is Kinematics
Kinematics is the branch of physics that deals with the motion of objects without considering the causes of motion. Among the various types of motion, uniform motion is a fundamental concept that provides a foundation for understanding more complex movements. In this article, we will delve into the intricacies of uniform motion, explore its characteristics, and see its applications in our daily lives.
What is Uniform Motion?
Uniform motion refers to the movement of an object at a constant speed in a straight line along specific fixed direction. In other words, the object covers equal distances in equal intervals of time, regardless of how small these intervals might be. This type of motion is characterized by:
- Constant Velocity: The speed/magnitude of velocity and direction of the object’s motion remain unchanged.
- Zero Acceleration: Since the velocity is constant, there is no change in speed or direction, resulting in zero acceleration.
As , \overrightarrow{v\;}\;=\;constan t\;
Therefore, \overrightarrow{a\;}=\;\frac{d\overrightarrow v}{dt}=\;0
Mathematical Representation
Consider an object is moving along +X axis with uniform velocity ‘v’ as shown in diagram. Assume that object is at position x=x_1 at time t=t_1 and reaches at position x=x_2 at time t=t_2
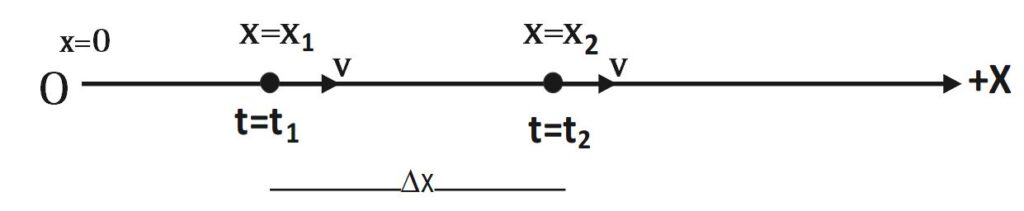
We know that velocity of object is defined as rate change of position of object w.r.t. time. Mathematically,
v=\frac{dx}{dt}\;
\Rightarrow dx\;=\;v\;dt\;
\int_{x_1}^{x_2}dx\;=\;\int_{t_1}^{t_2}v\;dt\;
\int_{x_1}^{x_2}dx\;=\;v\int_{t_1}^{t_2}\;dt\; (v= constant/uniform)
\left|x\right|_{x_1}^{x_2}=\;v\;\left|\;t\;\right|_{t_1}^{t_2}
x_2\;-x_1\;=\;v\;(t_2-t_1)
\Delta x\;=v\;\Delta t
v=\frac{\Delta x}{\Delta t}
Hence,\;v=\frac{dx}{dt}=\frac{\Delta x}{\Delta t}=constant
Clearly, uniform motion reflects that the object covers equal distances in equal intervals of time, regardless of how small these intervals might be.
When object/particle starts motion from origin (x=0)
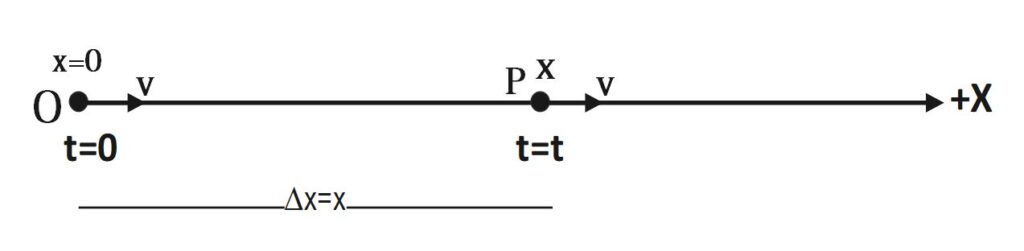
When particle starts motion from origin then initial displacement of particle is zero i.e. at t= 0 , x=0 . And it moves with constant velocity v, finally reaches at P in time t. Thus, at time t = t , x = x as shown in following diagram .
We know that for uniform motion,
\Delta x\;=v\;\Delta t
x-0= v(t-0)
x = v t
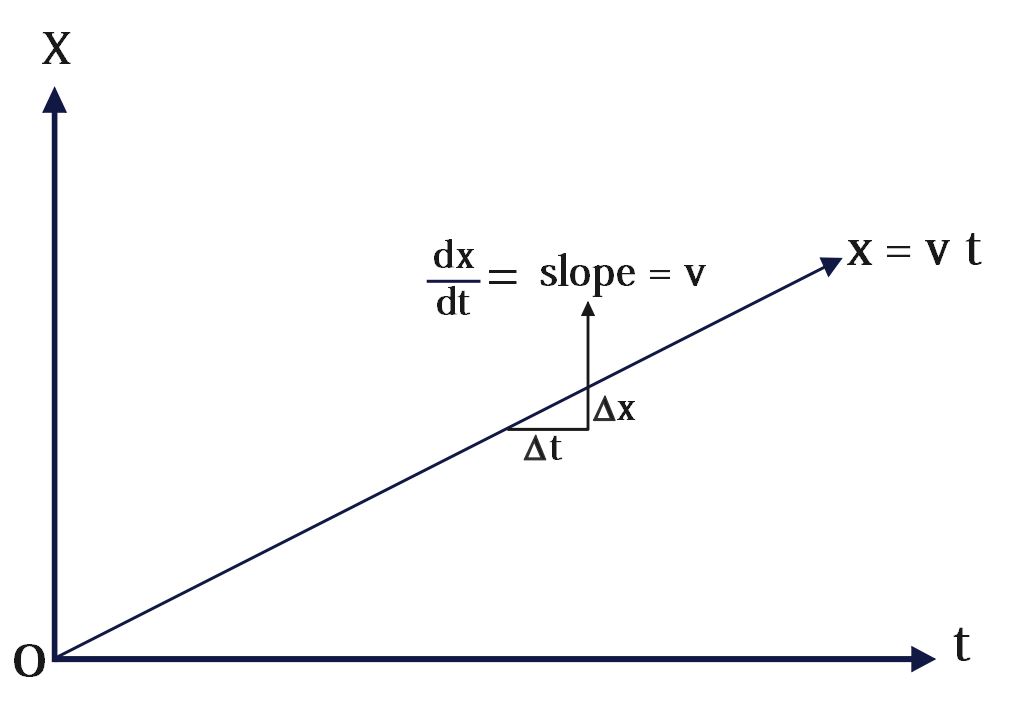
Position-Time (x-t) graph of uniform motion starting from origin
When object/particle starts motion with some initial displacement
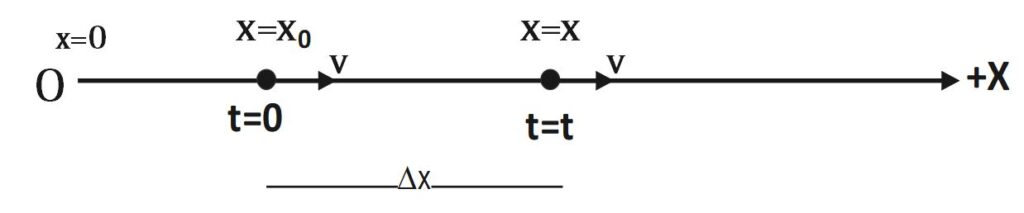
When particle does not starts motion from origin but from x= x_o then initial displacement of particle is non-zero i.e. at t=0 , x= x_o . With constant velocity v, it finally reaches at position x in time t as shown in following diagram . Thus, at time t = t , x = x
We know that for uniform motion,
\Delta x\;=v\;\Delta t
x-x_o= v(t-0)
x = x_o+ v t
Position-Time(x-t) graph of uniform motion of particle with non-zero initial displacement
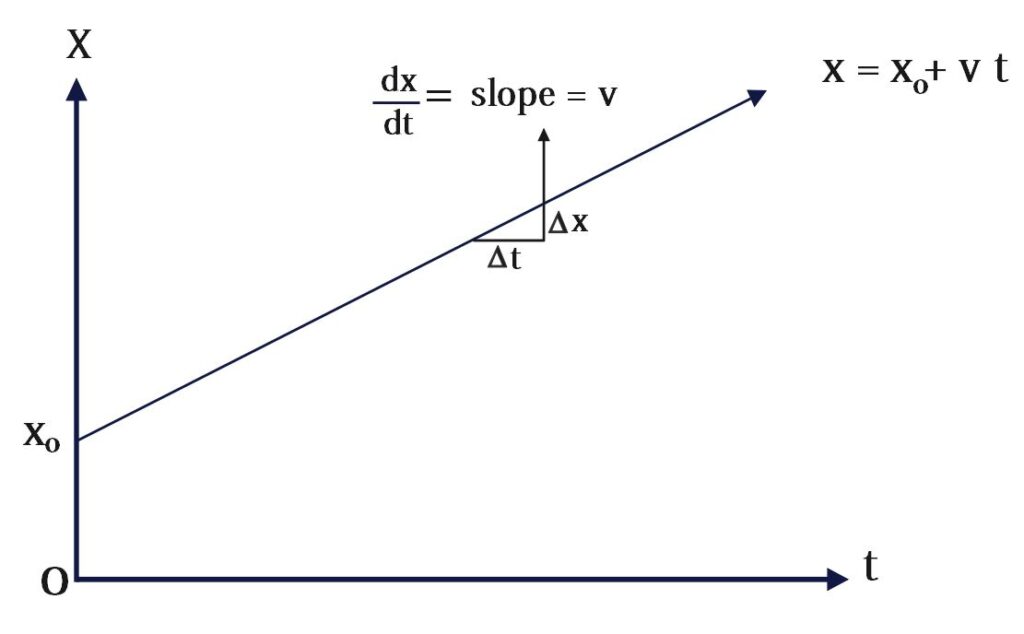
Graphical Representation
Position-Time Graph
In a distance-time graph for uniform motion, the distance (y-axis) plotted against time (x-axis) yields a straight line with a constant slope. The slope of this line equals the velocity of the object.
Velocity-Time Graph
In a velocity-time graph for uniform motion, the velocity (y-axis) plotted against time (x-axis) is a straight horizontal line. This horizontal line indicates that the velocity remains constant over time.
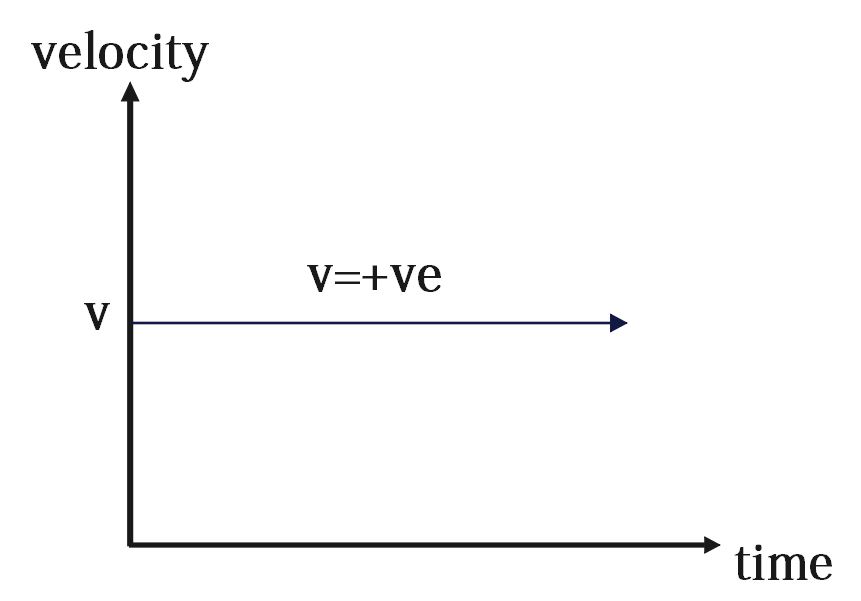
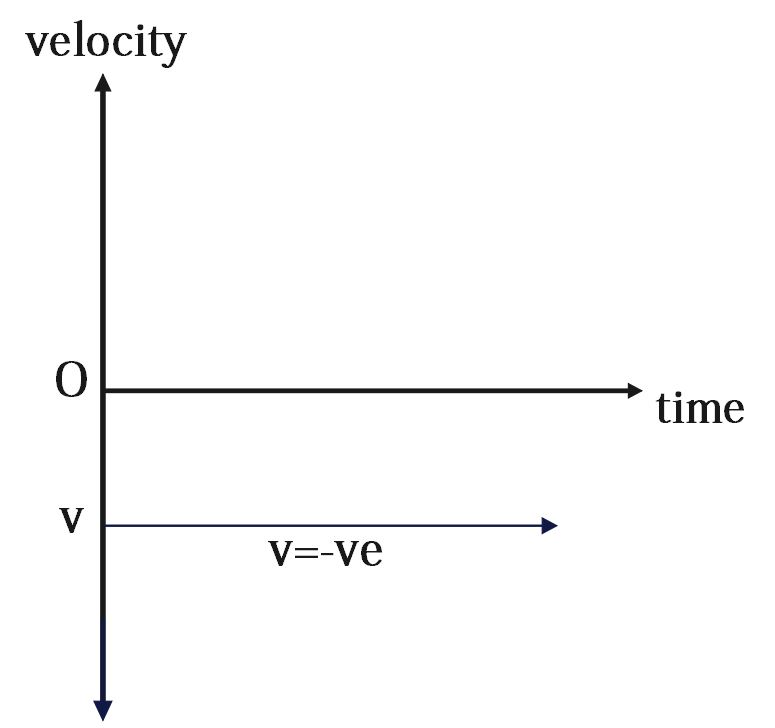
Uniform Motion vs. Non-Uniform Motion
Understanding the difference between uniform and non-uniform motion is crucial. While uniform motion features a constant velocity, non-uniform motion involves a change in speed or direction, indicating acceleration. Real-world motions are often non-uniform due to varying forces acting on objects, but uniform motion serves as an idealized model to simplify analysis.
Conclusion
Uniform motion, with its simplicity and predictability, is a cornerstone concept in kinematics. It lays the groundwork for more complex analyses of motion in physics and engineering. By grasping the fundamentals of uniform motion, one can better understand the intricate dynamics of moving objects, both in theoretical contexts and real-world applications. Whether it’s a car cruising on a highway or the precise movement of a spacecraft, uniform motion continues to be a vital principle in the study of mechanics.
