Force between the plates of capacitor
Introduction
Capacitors are fundamental components in electronics, used to store electrical energy. When a voltage is applied across the plates, an electric field develops, causing a charge to accumulate on the plates. The capacitor stores energy in the electric field created between the plates.
Among various types of capacitors, the parallel plate capacitor is one of the simplest and most widely studied. Understanding the force between the plates of a charged parallel plate capacitor not only deepens our comprehension of electrostatic principles but also has practical applications in various technologies.
Derivation of Force between the Plates of Capacitor
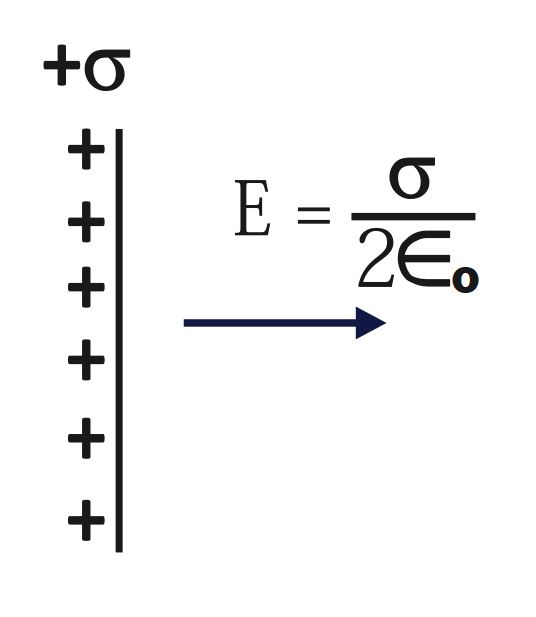
To derive the force between the plates, let us consider the small element of charge dq on second plate. Thus, calculate the force of attraction due to the electric field (of first plate) on small element of charge on second plate (-vely charged).
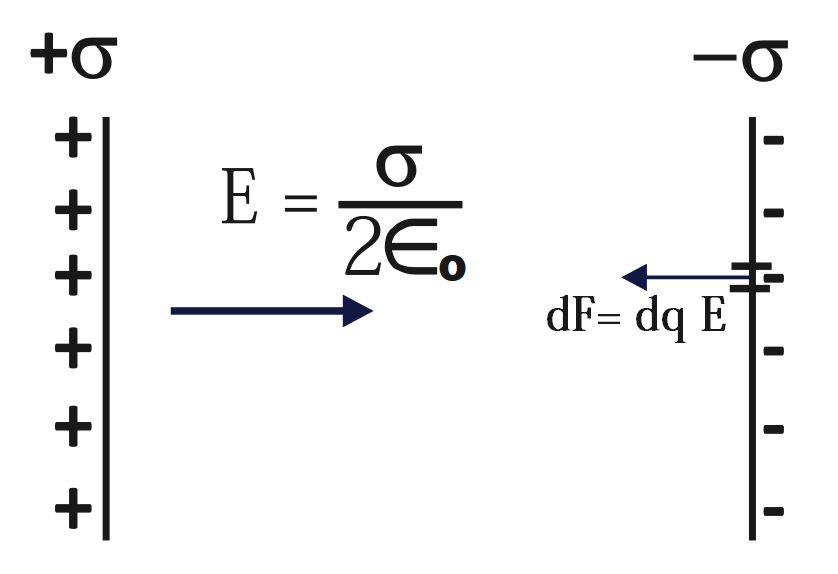
Force due to uniform electric field E on small element dq
dF\;=\;dq\;E
Integrating both sides
\int dF\;=\;\int dq\;E
F\;=\;E\;\int dq\; (As, E = constant)
F\;=\;E\;q
F\;=\;\left(\frac\sigma{2\in_o}\right)\;q
F\;=\;\left(\frac q{2A\in_o}\right)\;q
F\;=\frac{q^2}{2A\in_o}
Hence, we have obtained that the formula of force between the plates of capacitor
F\;=\frac{q^2}{2A\in_o}
Practical Implications
Understanding of the force between the plates of a capacitor is crucial for several reasons:
-
Mechanical Stability: In high-voltage applications, the force can be significant, potentially leading to mechanical deformation or even damage if the capacitor is not designed to handle such forces.
-
Design Considerations: Engineers need to consider this force when designing capacitors to ensure they remain stable and functional under varying electrical conditions.
-
Microelectromechanical Systems (MEMS): In MEMS devices, capacitors can be used as actuators where the force between plates is used to move microstructures.
