10 Important Problems for IIT-JEE and NEET
Problems 1 of "10 Important Problems for IIT-JEE and NEET"
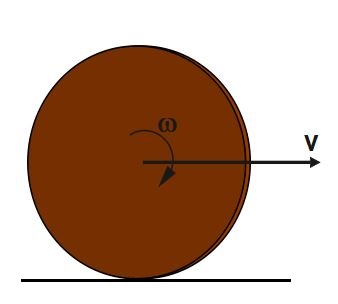
Q1.A solid disc is rolling without slipping on a horizontal ground as shown in figure. Its total kinetic energy is 150 J . Its translational and rotational kinetic energies respectively are
(A) 50 J , 100 J
(B)100 J , 50J
(C) 75 J, 75J
(D) 125J , 25J
Solution
As we know that, for pure rolling(without slipping) v=\;R\omega

\frac{K.E._R}{K.E_T}=\frac{{\displaystyle\frac12}I\;\omega^2}{{\displaystyle\frac12}m\;v^2}
\frac{K.E._R}{K.E_T}=\;\frac{\displaystyle\frac12\left(mK^2\right)\;\omega^2}{\displaystyle\frac12m\;v^2}
\frac{K.E._R}{K.E_T} =\frac{\displaystyle K^2\;\omega^2}{\displaystyle v^2}
\frac{K.E._R}{K.E_T}=\frac{\displaystyle K^2\;\omega^2}{\displaystyle{(R\omega)}^2}=\frac{\displaystyle K^2\;\omega^2}{\displaystyle R^2\;\omega^2}
\frac{K.E._R}{K.E_T}=\frac{\displaystyle K^2\;}{\displaystyle R^2\;}.......(1)
Now, I=\;\frac12m\;R^2=m\;K^2\; where\; K \;is \;radius\; of\; Gyration
\Rightarrow\frac{K^2}{R^2}=\frac12.......(2)
\Rightarrow\;\frac{K.E._R}{K.E_T}=\frac{K^2}{R^2}=\frac12 [from (1) and (2)]
\Rightarrow\;\frac{K.E._R}{K.E_T}=\frac12
\Rightarrow\ K.E_T=\;\left(\frac2{1+2}\right)\;K.E._{total}
\Rightarrow\ K.E_T=\;\left(\frac2{3}\right)\;*150
\Rightarrow\ K.E_T= 2* 50 = 100J
Similarly, K.E_R=\;\left(\frac1{1+2}\right)\;K.E._{total}
\Rightarrow K.E_R=\;\left(\frac1{1+2}\right)\;*150
\Rightarrow K.E_R=\;\left(\frac1{3}\right)\;*150
\Rightarrow K.E_R=1*50=50J
(B) is correct option
Problems 2 of "10 Important Problems for IIT-JEE and NEET"
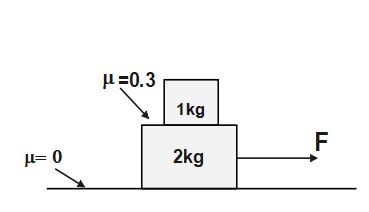
Q2.For given system of two blocks, find the maximum value of force F which can be applied on the system as shown in figure so that both blocks move together. [Given coefficient of static friction between both blocks = 0.3]
(A) 3N
(B) 6N
(C) 9N
(D) 12N
Solution
Free body diagram of block of upper block is
![For given system of two blocks, find the maximum value of force F which can be applied on the system as shown in figure so that both blocks move together. [Given coefficient of static friction between both blocks = 0.3]](https://pcmtutorials.in/wp-content/uploads/2024/02/block-fricition-2.jpg)
We can see that the block 1 Kg (upper block) is moved by friction force. If block moves together (without slipping) it means the frictional force is static friction. Therefore,
f_{s,max}=\;\mu_sN
f_{s,max}=\;\mu_s mg
f_{s,max}=\;\ 0.3 * 1 * 10 = 3N
f_{s,max}=\;\ 0.3 * 1 * 10 = 3N
Thus, maximum acceleration that can be produced in upper block without slipping is
a_{max}=\frac{f_{s,max}}m=\;\frac31=3ms^{-2}
For system of blocks , to move together the maxmium force can be
F_{max}=\;M_{sys,net\;}\ast\;\;a_{max}
F_{max}=(1+2) * 3= 9N
(C) is correct option
Problems 3 of "10 Important Problems for IIT-JEE and NEET"
Q3.What is the maximum compression in the spring, if the lower block is shifted to rightward with acceleration a. (Given that all surfaces are smooth as shown).
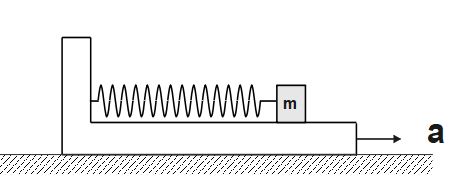
(A) \frac{ma}k
(B) \frac{2ma}k
(C) \frac{mak}2
(D) \frac{ma}{2k}
Solution
Let us assume that the upper block of mass 'm' displaces by distance 'x' towards leftward with velocity 'v' (w.r.t to lower block) when lower block is shifted towards rightward with acceleration a.
We can solve this problem by two method (1) Force Method (2) Energy Method from non-inertial frame of refence (Lower plank/block) .
Force Method
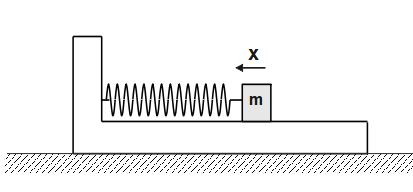
Acc. to Newton's 2nd law of motion,
F_{net}=F_{pseu}-F_{spring}
F_{net}=ma- kx
\frac{\operatorname dv}{\operatorname dt}=ma\;-\;kx
v\frac{\operatorname dv}{\operatorname dx}=ma\;-\;kx
v\;dv=\left(ma\;-\;kx\right)\;dx
Integrating both sides
\int_{v_i}^{v_f}\;vdv=\int_{x_i}^{x_f}\left(ma\;-\;kx\right)\;dx
\int_{0}^{0}\;vdv=\int_{0}^{x_o}\left(ma\;-\;kx\right)\;dx
\left[\frac{v^2}2\right]_0^0=\;ma\;\left[x\right]_0^{x_0}-k\left[\frac{x^2}2\right]_0^{x_o}
0-0=\;ma\;\left(x_o-0\right)-\;\frac12k\;\left(x_o^2-0\right)
0=\;ma x_o - \;\frac12k\ x_o^2
ma x_o = \frac12k\ x_o^2
2ma= k x_{o}
x_o=\frac{2ma}k
(B) is correct option
let a_1 be the acceleration of upper block w.r.t the lower block
FBD of upper block from lower block reference frame
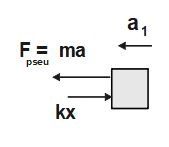
Boundary conditions for integration:
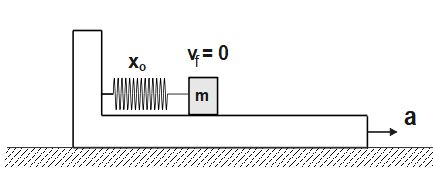
Initially, the upper block is at rest when x=0, therefore v_{i}=0
When the spring has maximum compression x_{o}, again the block becomes stationary w.r.t. lower block.
So, v_{f}=0 , when x=x_{o}
Alternate Method
We can also solve this problem by Energy Method from non-inertial frame of refence (Lower plank/block) . We will apply Work-Energy theorem from lower block frame of reference.
Energy Method
We can apply Work-Energy theorem for initial and final position of upper block w.r.t. lower block

Since, at initial position the upper block is at rest, therefore v_{i}=0
When the spring has maximum compression x_{o}, again the block becomes stationary w.r.t. lower block. So, also v_{f}=0
Acc. to Work-Energy Theorem,
F_{net}=ma- kx
W.D_{net \;by\;all\;forces}\;=\triangle K.E.\;
W.D._{pseudo}\;\;+\;W.D._{spring}\;=\;\frac12m\;v_f^2-\frac12m\;v_i^2
W.D._{pseudo}\;\;+\;W.D._{spring}\;=\;\frac12m\;v_f^2-\frac12m\;v_i^2
W.D._{pseudo}\;\;+\;W.D._{spring}\;=\;\frac12m\;*0^2-\frac12m\;*0^2
\Rightarrow\;ma\;x_o-\;\frac12k\;x_o^2=0
\Rightarrow\;ma\;x_o=\;\frac12k\;x_o^2
\Rightarrow\;ma\;=\;\frac12k\;x_o
\Rightarrow\;x_o=\frac{2ma}k
(B) is correct option
\;W.D._{cons}\;=-\triangle U
\;\Rightarrow\;W.D._{spring}\;=-\triangle U
\;\Rightarrow W.D._{spring}\;=-\;\frac12k\;x_{o}^2
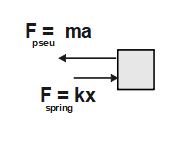
And, W.D._{pseu}={\overrightarrow{F\;}}_{pseu}.\overrightarrow{x_o}
\Rightarrow W.D._{pseu}=F_{pseu}\;x_{o\;}\cos0^o
\Rightarrow W.D._{pseu}=ma\;x_{o\;}
Problems 4 of "10 Important Problems for IIT-JEE and NEET"
Q4. A spaceship is launched into a circular orbit close to the earth's surface. What additional velocity has now to be imparted to the spaceship in the orbit to overcome the gravitational pull. Radius of earth =6400 km , g= 9.8 ms^{-2}
(A) 3.2 km/s
(B) 11.2 km/s
(C) 1.5 km/s
(D) 8 km/s
Solution
As we know that the speed of the spaceship in a circular orbit close to the earth's surface , v_o=\;\sqrt{gR}
Ans also, escape speed from earth's surface , v_e=\;\sqrt{2gR}
Additional velocity required to make spaceship escape,
v_{additional}= v_{e}- v_o= \;\sqrt{2gR}-\sqrt{gR}=\left(\sqrt2-1\right)\;\sqrt{gR}
v_{additional}=0.414 * 7.9= 3.27 km/s
(A) is correct option
Problems 5 of "10 Important Problems for IIT-JEE and NEET"
Q5. Moment of inertia of a uniform rod of length L and mass M, about an axis passing through L/3 from one end and perpendicular to its length is
(A) \frac2{27}M\;L^2
(B) \frac1{6}M\;L^2
(C) \frac1{12}M\;L^2
(D) \frac19M\;L^2
Solution
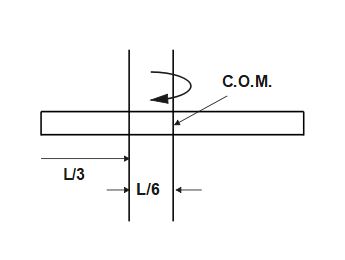
According to Parallel axis theorem ,
I_{parallel\;\;}=\;I_{COM}\;+\;M_{total\;}\;d^2
Here, d= perpendicular distance of parallel axis from the axis passing through C.O.M.
\;I_{COM}\; = Moment of Inertia of rod passing through C.O.M. (perpendicular to rod)
\Rightarrow\;I_{parallel}=\frac1{12}M\;L^2+\;M\;\left(\frac L6\right)^2
\Rightarrow\;I_{parallel}=\;ML^2\;\left[\frac1{12}+\frac1{36}\right]
\Rightarrow\;I_{parallel}=\;ML^2\;\left[\frac1{12}+\frac1{36}\right]
\Rightarrow\;I_{parallel}=\frac19M\;L^2
(D) is correct option
We have , I_{com}=\frac1{12}ML^2
And \;total\;mass\;of\;rod,\;M_{total}=M
d=\frac L2-\frac L3=\frac L6
Problems 6 of "10 Important Problems for IIT-JEE and NEET"
Q6.F-x equation of a body of mass 4 kg in S.H.M. is F+\;16x\;=0
Here, F is newton and x in meter. The time period of oscillations will be
(A) 6.28\; sec
(B) 3.14\; sec
(C) 1.57\; sec
(D) 1 \; sec
Solution
Given that, F+\;16x\;=0
Also, m= 4kg
F=\;-16x .......(1)
On comparing (1) and (2)
-kx= -16x
\Rightarrow\; k= 16
Time period of S.H.M. is T=2\pi\sqrt{\frac mk}
\Rightarrow T=2\pi\sqrt{\frac4{16}}
\Rightarrow T=2\pi\sqrt{\frac14}
\Rightarrow T=\frac{2\pi}2=\pi
\Rightarrow T=\pi=\;3.14\;sec
(B) is correct option
We already know, the equation of S.H.M. can be written as
F = -kx ......(2)
Problems 7 of "10 Important Problems for IIT-JEE and NEET"
Q7.A ball of mass m moving at a sped v makes a head on collision with an identical ball at rest. If the kinetic energy of the balls after collision is \frac34th of the original. Then the coefficient of restitution is
(A) e=\frac1{\sqrt2}
(B) e=\frac12
(C) e=\frac{\sqrt2}3
(D) e=\frac13
Solution
Given that, mass of each ball = m
According to law of conservation of momentum
m_1 u_1 +m_2 u_2 = m_1 v_1 + m_2 v_2
m v +m *0 = m v_1 + m v_2
m v = m (v_1 + v_2)
v = (v_1 + v_2)
v_1 + v_2 = v.....(1)
Given that , K.E._{net,f\;}=\frac34K.E._{net,i\;}
Therefore, \frac12\;m_1\;v_1^2\;+\;\frac12\;m_2\;v_2^2\;=\;\frac34\left[\frac12\;m_1\;u_1^2\;+\;\frac12\;m_2\;u_2^2\;\right]
\frac12\;m\;\left(\frac{v(1-e)}2\right)^2\;+\;\frac12\;m\;\left(\frac{v(1+e)}2\right)^2\;=\;\frac34\left[\frac12\;m\;v^2\;+\;\frac12\;m\;{\ast\;0}^2\;\right]
\frac12\;\;\frac{v^2\;\left(1+e\right)^2}4\;+\;\frac12\;\;\frac{v^2\;\left(1-e\right)^2}4\;=\;\frac34\left(\frac12\;v^2\;\right)
\Rightarrow\left(1+e\right)^2+\left(1-e\right)^2=3
\Rightarrow1+\;e^2+\;2e\;+\;1\;+\;e^2-2e\;= 3
\Rightarrow\;2\;e^2=\;1
\Rightarrow\;e^2=\;\frac12
\Rightarrow\;e=\;\frac1{\sqrt2}
(A) is correct option
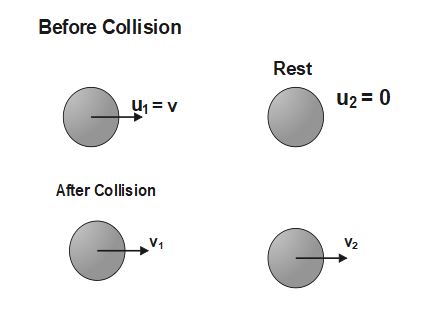
The formula of coefficient of restitution is :
e=\;\frac{vel. of sepration}{vel. of approach}
e=\;\frac{v_2-v_1}{u_1-u_2}
e=\;\frac{v_2-v_1}{v-0}
v_2- v_1= ev ....(2)
On adding (1) and (2), we get
2 v_2 = v +ev
v_2=\;\frac{v(1+e)}2
On subtracting (2) from (1), we get
2 v_1 = v - ev
v_1=\;\frac{v(1-e)}2
Problems 8 of "10 Important Problems for IIT-JEE and NEET"
Q8.The density of a rod AB increases linearly from A to B. Its mid-point is O and centre of mass is at C. Four axes pass through A, B, O and C , all perpendicular to the length of rod. The moments of inertia of the rod about these axes are I_{A}, I_{B}, I_{O} and I_{C} respectively. Then
(A) I_{A}> I_{B}
(B) I_{C} < I_{B}
(C) I_{O}> I_{C}
(D) All of these
Solution
Problems 9 of "10 Important Problems for IIT-JEE and NEET"
Q9.A simple harmonic oscillation has an amplitude A and time period T. The time required to travel from x=A\;to\;x=\frac A2 is
(A) \frac T4
(B) \frac T5
(C) \frac T6
(D) \frac T{12}
Solution
Problems 10 of "10 Important Problems for IIT-JEE and NEET"
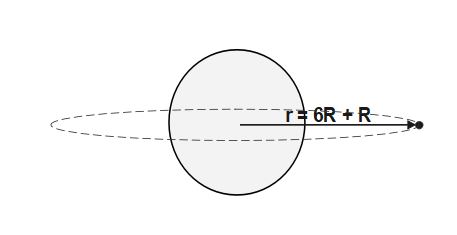
Q10. A geostationary satellite is orbiting the earth at a height of 6R above the surface of earth where R is the radius of earth. The time period of another satellite at a distance of 3.5 R from the centre of earth is
(A) 16.96 hours
(B) 8.48 hours
(C) 9.25 hours
(D) 15.76 hours
Solution
We know that , orbital speed of satellite is
v_o=\;\sqrt{\frac{GM}r}\;
where\;r\;is\;dis\tan ce\;from\;centre\;of\;planet/earth
T\;=\frac{dis\tan ce\;}{speed}=\;\frac{2\pi\;r}{v_o}
T\;=\;\frac{2\pi\;r}{\sqrt{\displaystyle\frac{GM}r}}
T\;=\;2\pi\;\sqrt{\frac{r^3}{GM}}
T\;=\;2\pi\;\sqrt{\frac{r^3}{GM}}\\T^2=\;4\;\pi^2\;\frac{r^3}{GM}
\Rightarrow T^2\;\;\propto\;r^3
This is known as Kepler's Law of period for planetary motion
r= R+ h where R is radius of planet/earth and h is height of satellite from surface of earth
\Rightarrow r_1 = R+ 6R=7R \;and \;r_2= 3.5R