Transient Current: Charging of Capacitor with DC source
Charging of Capacitor with DC source - IIT Advanced Topic
Transient Current :
Transient current is a temporary current that flows for a short, finite duration, starting from zero to a maximum value or from a maximum value to zero, in response to a sudden change in the circuit conditions, such as when a switch is turned on or off.
Charging of Capacitor : Introduction
Capacitor with DC source is practically CR circuit. In the capacitor charging there are three stages:
Initial Condition:
- When an uncharged capacitor is connected to a voltage source through a resistor, the transient current initially flows from zero to a maximum value.
Exponential Decay:
- The current then decreases exponentially over time as the capacitor charges, described by the equation:
I(t)\;=\;I_o\;e^{-\frac t{CR}}
where E is the applied voltage, R is the resistance, C is the capacitance, and 𝑡t is the time elapsed.
- The current then decreases exponentially over time as the capacitor charges, described by the equation:
Steady State:
- Once the capacitor is fully charged, the current drops to zero, indicating the end of the transient period.
I\;=\;\frac{dq_0}{dt}=\;o\;
- Once the capacitor is fully charged, the current drops to zero, indicating the end of the transient period.
Initial Condition
When switch is just closed, time, t=0 and capicitor is uncharged . So, Charge q=0
Also, intially the current will be maximum.
hence, I_o=\;\frac ER
Steady State
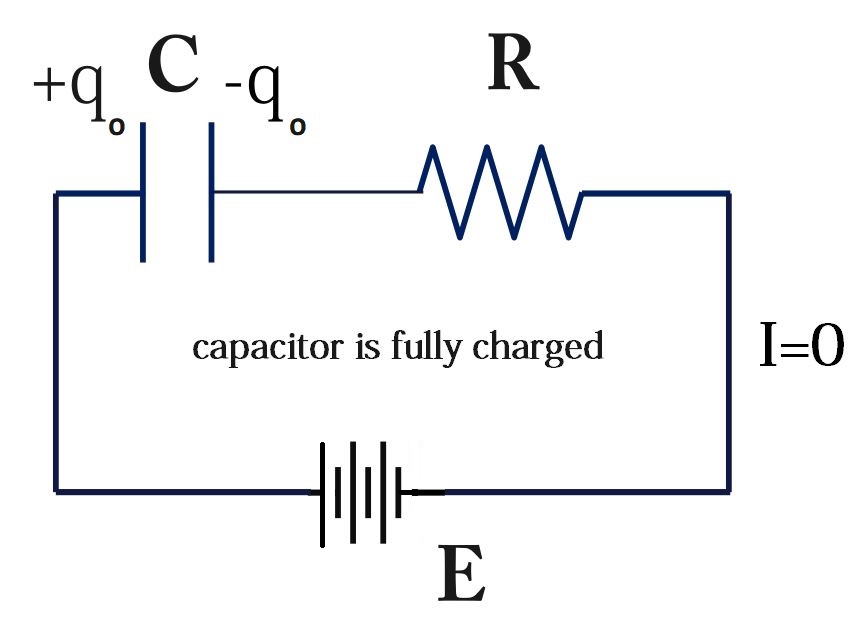
Capacitor continues getting charged until it is fully charged . This is called steady state.
As, we know that
I\;=\;\frac{dq_0}{dt}=\;o\;
where q_o is maximum charge
Therefore, according to Kirchhoff’s loop rule
E\;-\;\frac{q_o}C-(0)\;R=\;0E\;-\;\frac{q_o}C=\;0
E\;=\;\frac{q_o}C
q_o\;=\;EC…….(1)
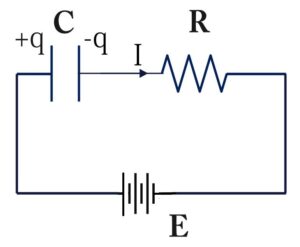
Assume that capacitor is charged up to charge q at any time t.
Therefore, time = t and charge = q
According to Kirchhoff's loop rule,
E-\;\frac qC-IR\;=\;0
EC-q-ICR\;=\;0
EC-q-\frac{dq}{dt}\;(CR)\;=\;0
q_o-q-\frac{dq}{dt}\;(CR)\;=\;0 [from(1)]
\frac{q_0-q}{CR}-\;\frac{dq}{dt}=0
\frac{q_0-q}{CR}=\;\frac{dq}{dt}
\frac1{CR}\;dt\;=\;\frac{dq}{q_o-q}\;
Integrating both sides
\int_0^t\frac1{CR}\;dt\;=\;\int_0^q\frac{dq}{q_o-q}\;
\frac1{CR}\int_0^t\;dt\;=\;\int_0^q\frac{dq}{q_o-q}\;
\frac1{CR}\;\left|t\right|_0^t\;\;=\;\;\left|\frac{\log_e\left(q_o-q\right)}{-1}\right|_0^q
\frac1{CR}(t-0)\;\;=\;\;-\;\lbrack\log_e\left(q_o-q\right)-\;\log_e\left(q_o-0\right)\rbrack
-\frac t{CR}\;=\;\;\;\log_e\left(\frac{q_o-q}{q_o}\right)
e^{-\frac t{CR}\;}\;=\;\frac{q_o-q}{q_o}
q_o\;e^{-\frac t{CR}\;}\;=\;q_o-q
\;q=q_o-\;q_o\;e^{-\frac t{CR}\;}\;
\;q=q_o(1-\;\;e^{-\frac t{CR}\;}\;)
q=\;q_o\;(1-e^{-\frac t\tau})
\tau = CR is called Time Constant
When time t=\;1\;\tau
So, q=\;q_o(1-\;e^{-1})\;=\;0.632\;q_o
Capacitor gets charged by 63.2% in first time constant
When time t=\;2\;\tau
So, q=\;q_o(1-\;e^{-2})\;=\;0.865\;q_o
Capacitor gets charged by 86.5% in two time constants
When time t=\;3\;\tau
So, q=\;q_o(1-\;e^{-3})\;=\;0.950\;q_o
Capacitor gets charged by 95% in three time constants
When time t=\;4\;\tau
So, q=\;q_o(1-\;e^{-4})\;=\;0.982\;q_o
Capacitor gets charged by 98.2% in four time constants
When time t=\;5\;\tau
So, q=\;q_o(1-\;e^{-5})\;=\;0.993\;q_o
Capacitor gets charged by 99.3% in five time constants
When steady state is attained, capacitor is fully charged
t\;\rightarrow\infty
q=\;q_o(1-\;e^{-\infty})\;
q=\;q_o(1-\;0)=\;q_o
So, q=\;q_o

\;q=q_o(1-\;\;e^{-\frac t{CR}\;}\;)
taking derivative both sides w.r.t. t
\frac{dq}{dt}=q_o\;\frac d{dt}(1-\;e^{-\frac t{CR}})
\frac{dq}{dt}=q_o\;\lbrack\;0-\;e^{-\frac t{CR}}\;\times\;(-\frac1{CR}\;)\;\rbrack
\frac{dq}{dt}=\;\frac{q_o}{RC}\;\;e^{-\frac t{CR}}\;
\frac{dq}{dt}=\;\frac{EC}{RC}\;\times\;e^{-\frac t{CR}}\;
\frac{dq}{dt}=\;\;\frac ER\;\times\;e^{-\frac t{CR}}\;
I=\;\;I_o\;\times\;e^{-\frac t{CR}}\; [ From (1) ]
I=\;\;I_o\;\;e^{-\frac t{CR}}\;
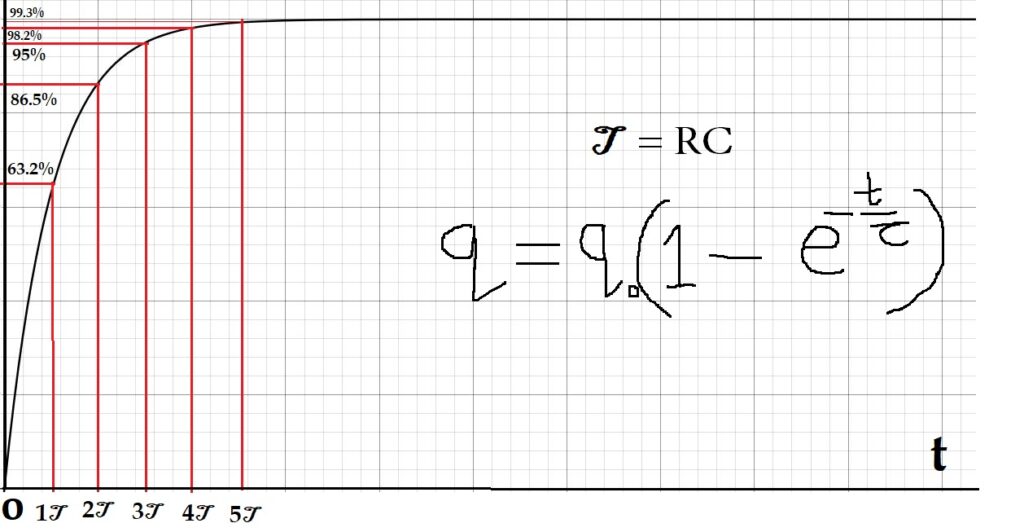
Exponential Growth of Charge : Charging of Capacitor
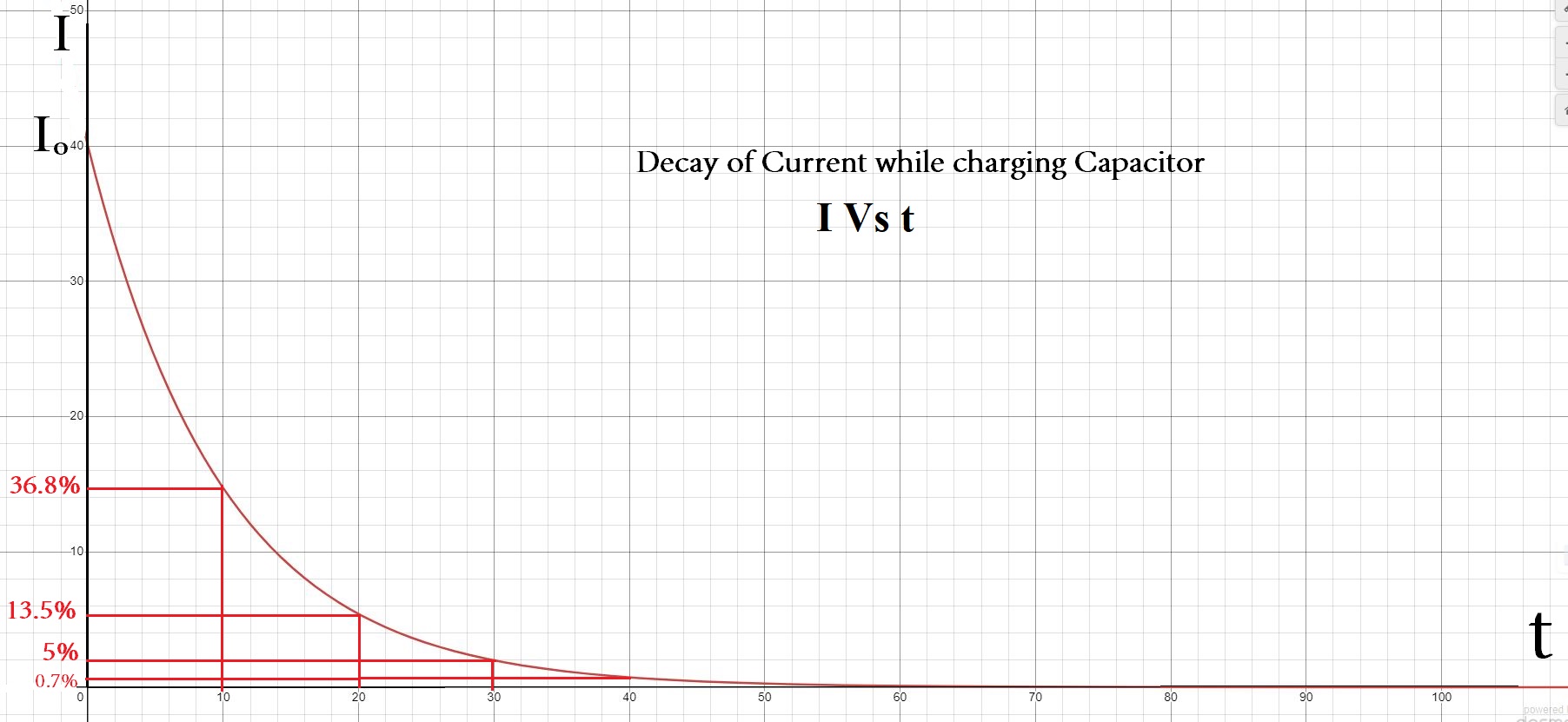
Exponential Decay of Current : Charging of Capacitor
I=\;\;I_o\;\;e^{-\frac t{CR}}\;
I=\;I_o\;e^{-\frac t\tau}
I=\;I_o\;e^{-\frac t\tau}
When time t=\;1\;\tau
I=\;\;I_o\;e^{-1}\;
I=\;0.368\;I_o\;
So, current reduces by 62.8% of maximum current in 1 time constant
When time t=\;2\;\tau
I=\;\;I_o\;e^{-2}\;
I=\;0.135\;I_o\;
So, current reduces by 86.5% of maximum current in 2 time constants
When time t=\;3\;\tau
I=\;\;I_o\;e^{-3}\;
I=\;0.05\;I_o\;
So, current reduces by 95% of maximum current in 3 time constants
When time t=\;4\;\tau
I=\;\;I_o\;e^{-4}\;
I=\;0.018\;I_o\;
So, current reduces by 98.2% of maximum current in 3 time constants
When time t=\;5\;\tau
I=\;\;I_o\;e^{-5}\;
I=\;0.07\;I_o\;
So, current reduces by 99.3% of maximum current in 3 time constants
When steady state is achieved , then current reduces to zero
t\;\rightarrow\infty
I=\;\;I_o\;e^{-\infty}\; =0
Charging of Capacitor : An Overview
Initially, when switched is just on , capacitor is is uncharged and it offers zero resistance to DC source and current is maximum(largest possible). Thus, we can calculate the value of maximum current by formula, I_o=\;\frac ER
Finally, steady state is attained after some time (theoretically , when t\;\rightarrow\infty ) and capacitor gets fully charged. Now, capacitor starts blocking DC (direct current) and it reduces to zero i.e. I = 0
Consequently, maximum charge is q_o\;=\;EC
During charging of capacitor , current falls from I_o to 0 . This is known as decay of current. It is found that the decay of current is exponential decay as according to formula I=\;\;I_o\;\;e^{-\frac t{CR}}\;
Numerical based on Charging of Capacitor
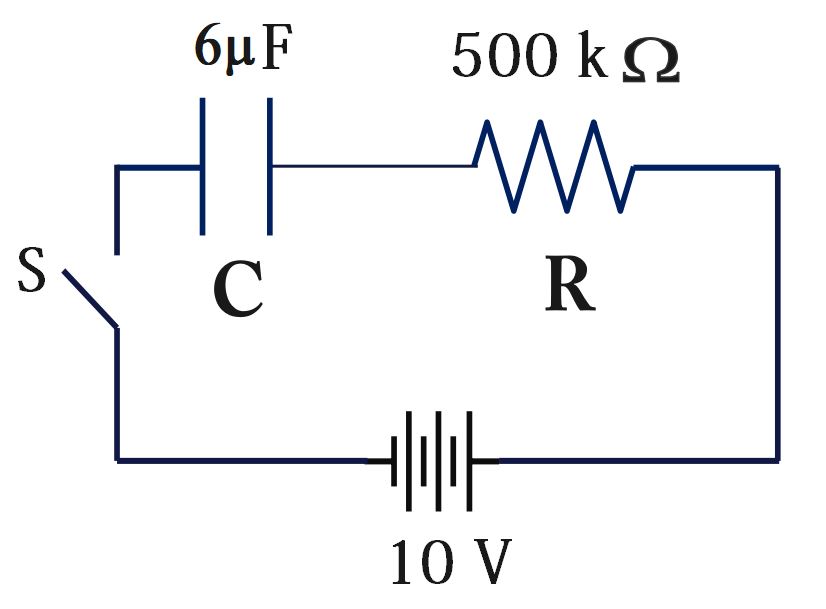
Ex. An uncharged capacitor and a resistor are connected in series, as shown in the figure below. The emf of the battery is ε = 10 V, C = 6 μF, and R = 500 kΩ.
After the switch is closed, find
(a) The time constant of the RC circuit.
(b) The maximum charge on the capacitor.
(c) The charge on the capacitor 6 s after the switch is closed.
(d) The charge on the capacitor 8.1 s after the switch is closed.

Pingback: Force between the plates of capacitor