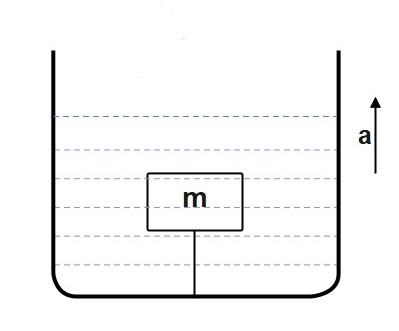
A block of mass 1 kg and density 0.8 g/cm^3 is held stationary with the help of a string as shown in figure. The block is completely immersed into the water filled in tank.If the tank is accelerating vertically upwards with an acceleration a = 2 m/s^2.
(i) Find the tension in the string.
(A) 3 N
(B) 2 N
(C) 3.5 N
(D) 5.5 N
Solution
Let V = Volume of body
\rho = density of block = 0.8 \frac{g}{cm^3}=800\frac{kg}{m^3}
\sigma = density of water =1000\frac{kg}{m^3}
We know that, the mass of block= m=\;\rho\;V
\rho=\frac mV
V=\frac m\rho
We know that F_{up}=V\sigma(g+a)\;
\Rightarrow F_{up}=\frac m\rho\sigma(g+a)\;
\Rightarrow F_{up}=\frac1{800}\ast1000\ast(10+2)=15N
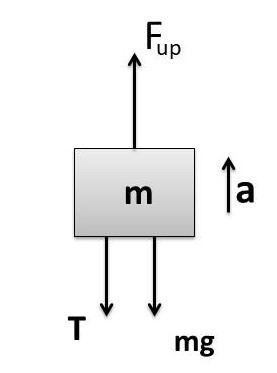
According to Newton's 2nd law of motion, we can write
F_{net}= F_{up}-T- mg
ma= F_{up} -T- mg
1*2= 15-T-1*10
2= 15 - T- 10
T= 15 - 10-2=3N
(A) is correct option
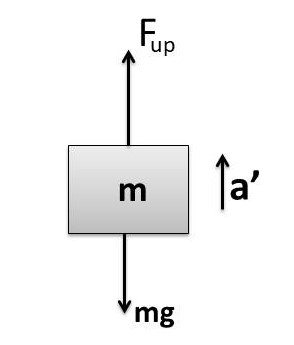
(ii) Determine the acceleration produced in the of block when the string is cut off.
(A) 3 ms^{-2} downwards
(B) 3 ms^{-2} upwards
(C) 2 ms^{-2} upwards
(D) 5 ms^{-2} upwards
When string is cut off then T=0 and the block will move upwards due to upwards force as density of block is lesser than that of water.
We know that, the acceleration = a^{'}=\frac{F_{net}}m
a^{'}=\frac{F_{up}-mg}m=\;\frac{15-1\ast10}1=\frac{15-10}1=5\;ms^{-2}
(D) is correct option