Moment of Inertia of Rod having non-uniform, linearly increasing mass density
Moment of Inertia
Moment of inertia is of great importance when we come to discuss the rotational dynamics. The the word “inertia” refers to resistance against any change in state of object (mass). Specifically, the moment of inertia is measure of a body’s resistance to changes in its rotation. The greater the value of moment of inertia, the more is difficulty it is to cause change in its rotation.
The moment of inertia is often denoted as “I” and it is analogous to mass (m) of the object. In linear motion, mass quantifies an object’s resistance to linear acceleration (change in velocity) in response to a force. Similarly, in rotational motion, the moment of inertia quantifies an object’s resistance to angular acceleration (change in angular velocity) in response to a torque. Moreover, both are scalar quantities.
Factors affecting Moment of Inertia
Here are the main factors affecting the moment of inertia:
Mass Distribution
Shape of the Object
Axis of Rotation
Size and Dimensions
- Symmetry
Infact, we can can generalize the above all factor into one key factor – the mass distribution of body about axis of rotation which incorporates he definition of moment of inertia.
I= m_1 r_1^{2} + m_2 r_2^{2}+ …… m_n r_n^{2} . Lets consider following example to grasp the concept of moment of inertia.
Example - On Moment of Inertia of Rod
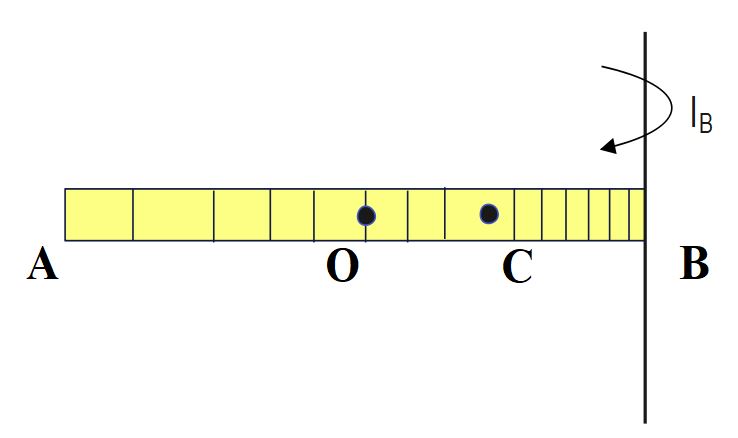
The density of a rod AB increases linearly from A to B. Its mid-point is O and centre of mass is at C. Four axes pass through A, B, O and C , all perpendicular to the length of rod. The moments of inertia of the rod about these axes are I_{A}, I_{B}, I_{O} and I_{C} respectively. Then
(A)I_{A}> I_{B}
(B)I_{C}< I_{B}
(C)I_{O}> I_{C}
(D) All of these
Solution
The mass distribution of body about axis of rotation determine the value of moment of inertia.
I= m_1 r_1^{2} + m_2 r_2^{2}+ …… m_n r_n^{2} .
If the overall mass is distributed nearer to axis of rotation then M.O.I. of the object(rigid body) will be smaller. And if mass is distributed away from axis of rotation it results into larger M.O.I.
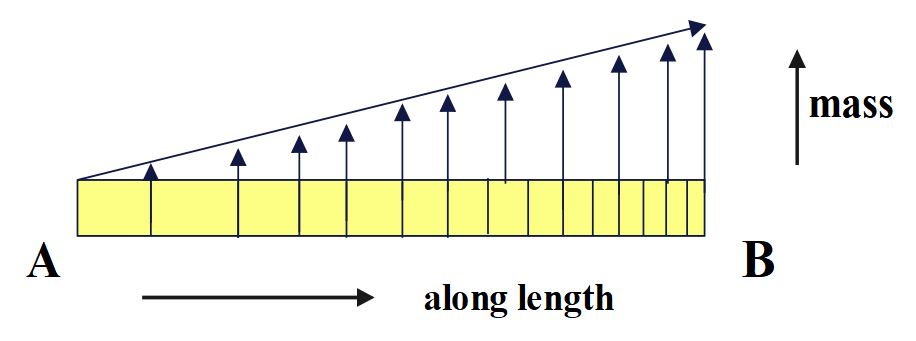
Let us first locate the center of mass (C.O.M.) of the rod by using formula:
\\x_{com}=\;\frac{\int_0^Ldm\;x}{\int_0^Ldm}=\frac{\int_0^Ldm\;x}M ….(1)
Given that ,the linear mass density of the rod varies linearly along the length as \lambda\;=\lambda_o\;x
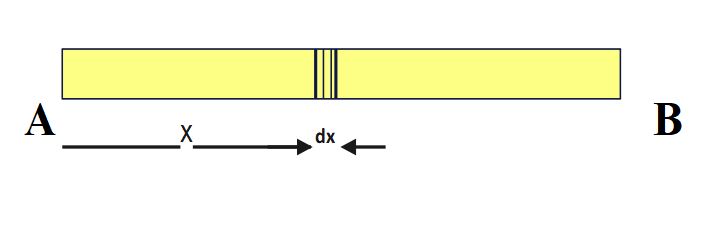
Mass of the small element dx, dm= \lambda\ dx
By integrating on both sides, we can calculate total mass of the rod
M=\lambda_o\;\left|\frac{x^2}2\right|_0^L=\;\frac12\lambda_o\;L^2….(2)
Now, we have to calculate , \int_0^Ldm\;x\;
\Rightarrow\;\int_0^Ldm\;x\; =\;\;\frac{\;\lambda_o\;L^3}3….(3)
From(1),(2)and (3)
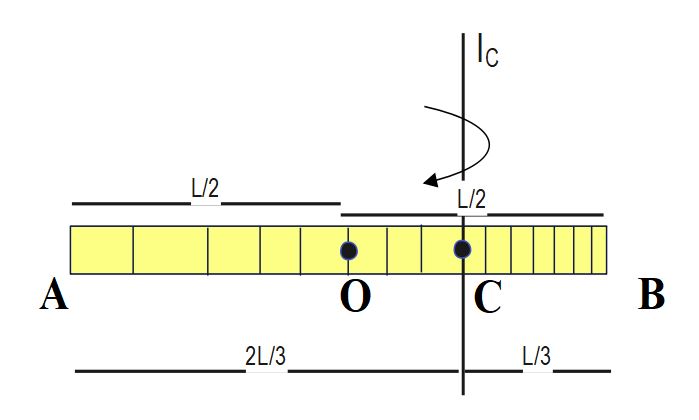
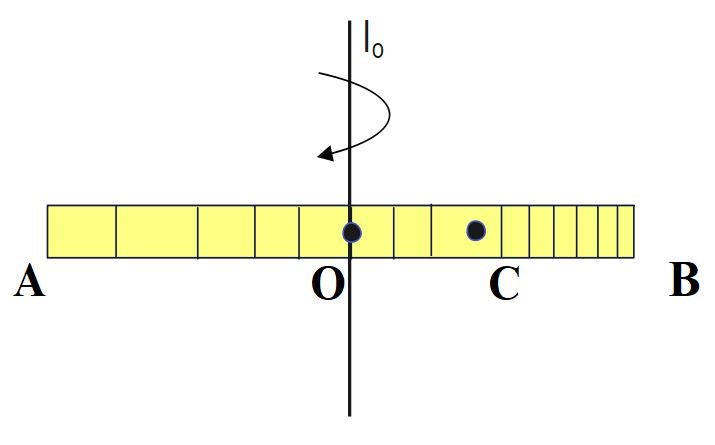
According to Parallel axis theorem ,
I_{parallel\;\;}=\;I_{COM}\;+\;M_{total\;}\;d^2
I_{O\;\;}=\;I_{C}\;+\;M \;(OC)^2
I_{B\;\;}=\;I_{C}\;+\;M \;(BC)^2
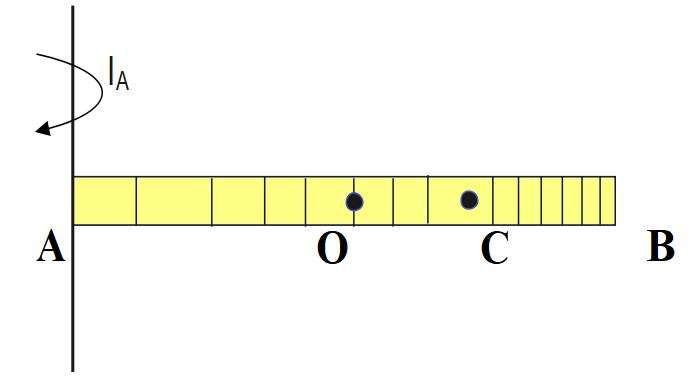
I_{A\;\;}=\;I_{C}\;+\;M \;(AC)^2
AC = 2L/3 , BC = L/3, OC= L/6
As, AC > BC> OC
Hence, I_A> I_B>I_O> I_C
(D) is correct option
Conclusion-
In case of variable mass density total mass can be calculated by integration. And apply formula x_{com}=\;\frac{\int dm\;x}{\int dm} to find position/coordinate of center of mass. Understanding of parallel axis theorem is key concept which relates all moment of inertias about any parallel axis with axis passing through centre of mass. Distribution of mass away from axis of rotation leads to greater value of moment of inertia about that axis.