Kepler's law of period
Kepler's law of period for planetary motion
According to Kepler’s laws of period for planetary motion, the square of the period of revolution of as planet around the sun is directly proportional to the cube of the semi-major axis of its orbit.
Mathematically, it can be expressed as T^2 = k a^3 , where �T is the orbital period of the planet, �a is the semi-major axis of its orbit, and �k is a constant that is the same for all planets orbiting the Sun.
Example
Q.A geostationary satellite is orbiting the earth at a height of 6R above the surface of earth where R is the radius of earth. The time period of another satellite at a distance of 3.5 R from the centre of earth is
(A) 16.96 hours
(B) 8.48 hours
(C) 9.25 hours
(D) 15.76 hours
Solution
We know that , orbital speed of satellite is
v_o=\;\sqrt{\frac{GM}r}\;
where\;r\;is\;dis\tan ce\;from\;centre\;of\;planet/earth
T\;=\frac{dis\tan ce\;}{speed}=\;\frac{2\pi\;r}{v_o}
T\;=\;\frac{2\pi\;r}{\sqrt{\displaystyle\frac{GM}r}}
T\;=\;2\pi\;\sqrt{\frac{r^3}{GM}}
T\;=\;2\pi\;\sqrt{\frac{r^3}{GM}}\\T^2=\;4\;\pi^2\;\frac{r^3}{GM}
\Rightarrow T^2\;\;\propto\;r^3
This is known as Kepler's Law of period for planetary motion
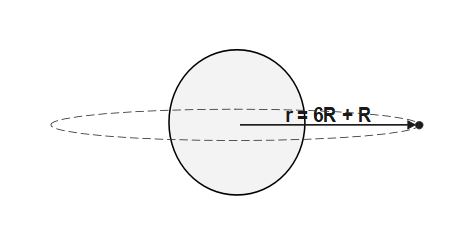
r= R+ h where R is radius of planet/earth and h is height of satellite from surface of earth
\Rightarrow r_1 = R+ 6R=7R \;and \;r_2= 3.5R
\Rightarrow T\;\propto\;r^\frac32
\frac{T_2}{T_1}=\;\left(\frac{r_2}{r_1}\right)^\frac32
\frac{T_2}{T_1}=\;\left(\frac{3.5R}{7R}\right)^\frac32
\frac{T_2}{T_1}=\;\left(\frac{1}{2}\right)^\frac32
\frac{T_2}{T_1}=\frac1{2\sqrt2}
T_2 =T_1 * \frac1{2\sqrt2}
T_2 =24 * \frac1{2\sqrt2}
T_2 =12* \frac1{\sqrt2}
T_2 =12* 0.707= 8.48 \;hours
(B) is correct option
Conclusion
Kepler’s third law is also known as law of period which helps us to find the time period of orbital motion for various distances from sun. It includes following applications.
Predicting Planetary Motion: Kepler’s law of periods allows astronomers to predict the orbital periods of planets based on their distances from the sun. This law has been crucial in the study of our solar system and in the discovery and characterization of exoplanets in other solar systems.
Comparing Orbits: By comparing the orbital periods and semi-major axes of different planets or moons, astronomers can gain insights into the structure and dynamics of planetary systems. For example, comparing the orbital periods of moons around a planet can provide information about their relative distances from the planet.
Verification of Kepler’s Laws: Kepler’s laws of planetary motion played a significant role in the development of Newton’s law of universal gravitation and the laws of motion. They served as a crucial test for Newtonian physics and provided evidence for the gravitational force between celestial bodies.