A small body of density ρ is dropped from rest at a height h into a lake of density σ , where σ > ρ . What would be of the acceleration of body till it moves inside the lake? (Neglect all dissipative effects)
(A) g\left(\frac\sigma\rho-1\right)\;downwards
(B) g\left(\frac\sigma\rho-1\right)\;upwards
(C) g\left(\frac\sigma\rho\right)\;downwards
(D) g\left(\frac\sigma\rho\right)\;upwards
Solution
Let V = Volume of body
\rho = density of body
\sigma = density of lake water
Thus, m=\;\rho\;V
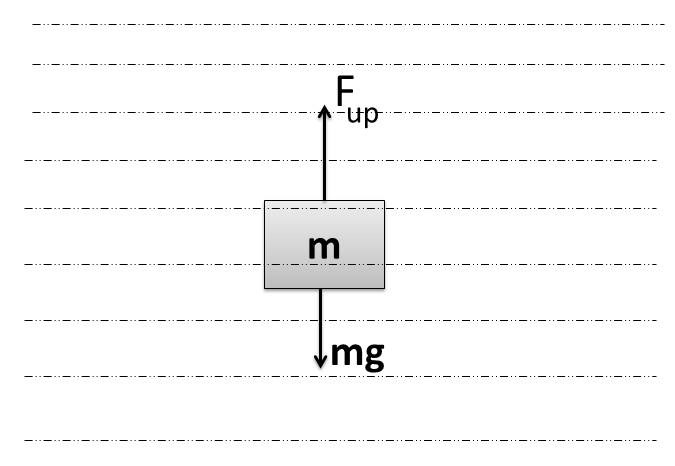
As the density of liquid is more than that of body( σ > ρ), Therefore the body has tendency to float on the liquid because of larger upwards force in comparison to that of weight of body. Hence, net force will be upwards.
W know that F_{up}=V\;\sigma g\;
According to Newton's 2nd law of motion, we can write
F_{net}= F_{up}-mg (upwards)
F_{net}= V\sigma g -V \rho g
ma = V\sigma g -V \rho g
V\rho a = V\sigma g -V \rho g
a=\frac{V(\sigma-\rho)g}{V\rho}
a=\frac{(\sigma-\rho)g}{\rho}
a=g\left(\frac\sigma\rho-1\right)\;upwards
(B) is correct option