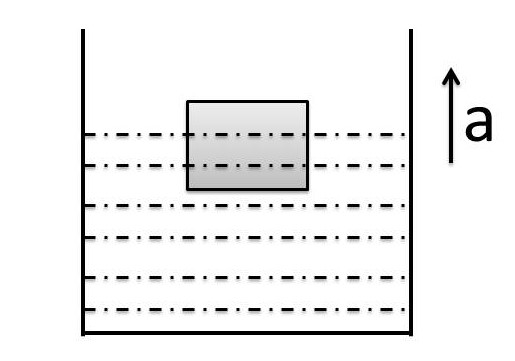
Q.A partially immersed solid block of density \rho_s is floating in a liquid of density \rho_L as shown in figure. If beaker container moves up with positive acceleration 'a' , what is correct statement about the block ?
(A) It sinks more
(B) It sinks lesser
(C) It neither sinks more nor lesser
(D) Cannot be predicted as data is insufficient
Solution
Let V_{in} = Volume of block immersed in the liquid
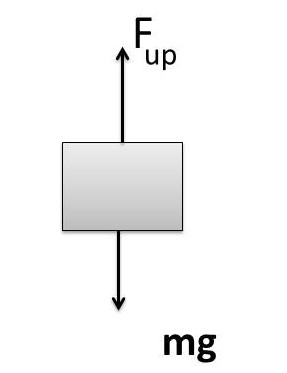
For Equilibrium of rest, see FBD as shown aside
F_{up}=V_{in}\;\rho_Lg\;=\;mg
V_{in}\;\rho_Lg\;=\;V\;\rho_S\;g\;
\;\frac{V_{in}}V\;=\frac{\rho_S}{\rho_L}
Therefore, fraction of volume inside the liquid is-
\;\frac{V_{in}}V\;=\frac{\rho_S}{\rho_L}.....(1)
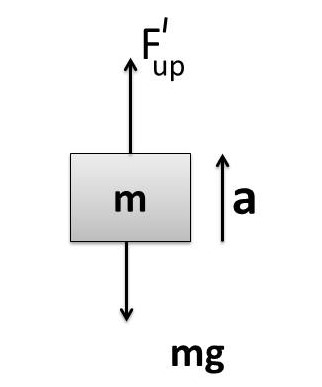
When block is moving up , the FBD is shown in figure
\;\\F_{up}^I=V_{in}^I\;\rho_L\;g_{eff}\\
F_{up}^I=V_{in}^I\;\rho_L\;(g+a).....(2)
F_{net}=F_{up}^I-mg
ma =F_{up}^I-mg
F_{up}^I=m(g+a)
F_{up}^I=V\;\rho_S\;(g+a)\\....(3)
From (2) and (3), V_{in}^I\;\rho_L\;(g+a)=V\;\rho_S\;(g+a)
\;\frac{V_{in}^I}V\;=\frac{\rho_S}{\rho_L}
\;\frac{V_{in}}V\;=\frac{\rho_S}{\rho_L}=\;\frac{V_{in}^I}V\;
Hence, fraction of volume immersed is again equal to \frac{\rho_S}{\rho_L}. It means immersed volume remains same .
Ans. (C) is correct option
Actually, this question is all about the Archimedes Principle which focus on the concept of Upthrust/Buoyant force acting on completely or partially immersed solid block or any other solid/hollow object. It helps in calculating the loss of weight when any solid substance is partially or completely immersed into the liquid. The liquid container may be stationary or moving with constant velocity/ variable velocity.
When completely or partially immersed solid block lies in stationary beaker container :-
When beaker container is stationary then , according to Archimedes Principle , it loses its weight to equal to the weight of liquid displaced by the object (like completely or partially immersed solid block) . Therefore,
F_{up}=V_{in}\;\rho_Lg\;=\;mg
When completely or partially immersed solid block lies in beaker container moving up with constant acceleration :-
When beaker container is moving up with uniform acceleration, then the loss of weight of object is now equal to apparent weight of liquid displaced by it.Thus, buoyant force/ upthrust changes so as to balance the increased effective weight of solid block when it observed from frame of reference of accelerated beaker.
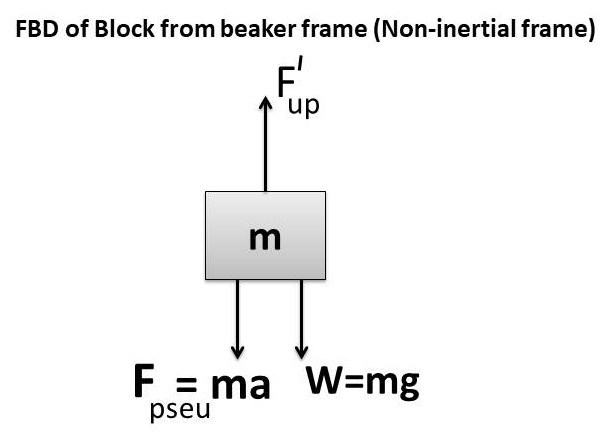
F_{up}^I=F_{pseu}+W
F_{up}^I=ma\;+\;mg
F_{up}^I=m(g\;+\;a)
F_{up}^I=mg_{eff} where g_{eff}=g+a
Therefore, we can write
\;\\F_{up}^I=V_{in}\;\rho_L\;g_{eff}\\
F_{up}^I=V_{in}\;\rho_L\;(g+a)
Conclusion-
From the above discussion, we understand that the volume immersed does not change when the container accelerates uniformly upwards or downwards along vertical. Immersed part remains same. Block neither sinks more nor lesser. This problems is best combine of Newton’s laws of motion, Archimedes’s Principle and Law of Flotation. This is how we reach to the conclusion that the knowledge of Free Body Diagram and Pseudo force is necessary to get into problems solving process. In fact the basic idea of pseudo force can be summarized into one line that a problem which is solved by application Newton’s 2nd law (from ground frame) gets converted into problem of Equilibrium of rest (from non-inertial frame of reference) by introducing concept of pseudo force.
Pseudo force can be written as:
{\overrightarrow{F\;\;}}_{pseu}=-M_{object}\;\;{\overrightarrow{a\;\;}}_{frame}
The negative sign shows that the peudo force is taken opposite to direction of acceleration of non-inertial frame.
Law of flotation simply gives us the condition under which an object floats partially or completely immersed inside the liquid. It suggest that
(i) if the density of solid is lesser than density of liquid then it floats partially immersed in the liquid
(ii) if the density of solid is equal to the density of liquid then it floats completely immersed in the liquid
(iii) if the density of solid is more than the density of liquid then it sinks completely unitl it settles down to bottom of container.
It is very interesting to note that this law also helps to find out fraction of immersed volume of object inside the liquid. We have to understand the relationships between different concepts of mechanics to solve such type of fluid mechanics problems.