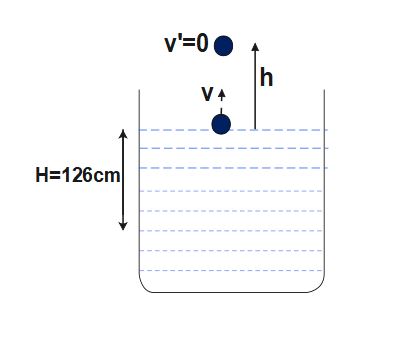
A wooden ball of density 900 kg / m^{3} is immersed in a liquid of density 1200 kg / m^{3} to a depth of 126 cm and the released. The height h above the surface of which the ball rises will be
(A) 40 cm
(B) 42 cm
(C) 45 cm
(D) 50 cm
Solution
Let V = Volume of ball
Given that, \rho = density of wooden ball= 900\frac{kg}{m^3}
\sigma = density of liquid =1200\frac{kg}{m^3}
As, the density of wooden ball = \rho=\frac mV
m=V\rho
We know that F_{up}=V\sigma g\;
According to Newton's 2nd law of motion, we can write
F_{net}= F_{up}-mg
ma= V\sigma g - V\rho g
V\rho a= V\sigma g - V\rho g
a=\;\frac{V\sigma g-V\rho g}{V\rho}
a=\;\frac{(\sigma-\rho)g}\rho
a=\;\frac{(1200-900)g}{900}
a=\;\frac{(300)g}{900}
a=\;\frac{g}{3}
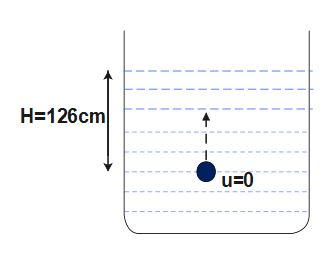
Now, u=0 (because the ball is released from rest)
When ball reaches to surface, S= 126 cm = 1.26 m. Also, let us assume that it attains velocity v at top surface.
According to Kinematics Equation of U.A.M., v^2-u^2=2aS
\Rightarrow v^2-0^2=2\left(\frac g3\right)\;\left(1.26\right)
\Rightarrow v^2=0.84 g .....(1)
h= height the wooden ball attains when it rises up with velocity v from top surafce
Since , the wooden ball rises up vertically under the effect of gravity, so it would come to rest momentarily when it attains height 'h'
v^{'}=0
A =-g
(-ve sign appears as the diraction of acceleration is against motion)
Again,apply V^2-U^2=2AS
\Rightarrow\;v'^2-v^2=2(-g) h
\Rightarrow\;0^2-v^2=2(-g) h
\Rightarrow\ v^2=2gh ....(2)
From (1) and (2), we get,
0.84g = 2gh
h=\frac{0.84g}{2g}
h=0.42m=42cm
(B) is correct option